Route Progress Algorithm

Updated: As of 12/08/2022

This is incomplete, but it’s the basic framework for determining a bus’s progress along a route. The calculation is performed with the assumption that the bus is near a valid route at all times:

The current issue lays in the fact that the bus location aggregation algorithm is not an accurate assessment of the actual location of the bus. Therefore the bus fails the check for determining whether the bus is within an acceptable distance of one of the possible routes.

The current implementation of the algorithm thus depends on tweaking the variable isOnRouteThreshold within Utilities.Swift

	static let isOnRouteThreshold: Double = 5

Making this variable greater relaxes the bounds we set on the accuracy of the bus location data and is therefore more prone to giving incorrect results due to noise.

Making this variable smaller makes the bounds we set on the accuracy of the bus location data more strict and is therefore more prone to causing the algorithm to end early and return nothing after detecting the bus is not close enough to one of the possible routes.

Therefore, there is a trade-off. However, one possible solution to improve the accuracy of the bus location data while providing strict checks to avoid incorporating buses too far from any given route is to implement the Kalman Filter for optimally estimating the location of the bus and reducing noise.

Note that as of 12/08/2022 the Kalman Filter is not yet implemented while the algorithm below has already been completed.

1. Find the route closest to the bus

1. Iterate over all routes from route_1, route_2, ... route_n. (As of 12/6/2022 there are only two routes: West Route, North Route).
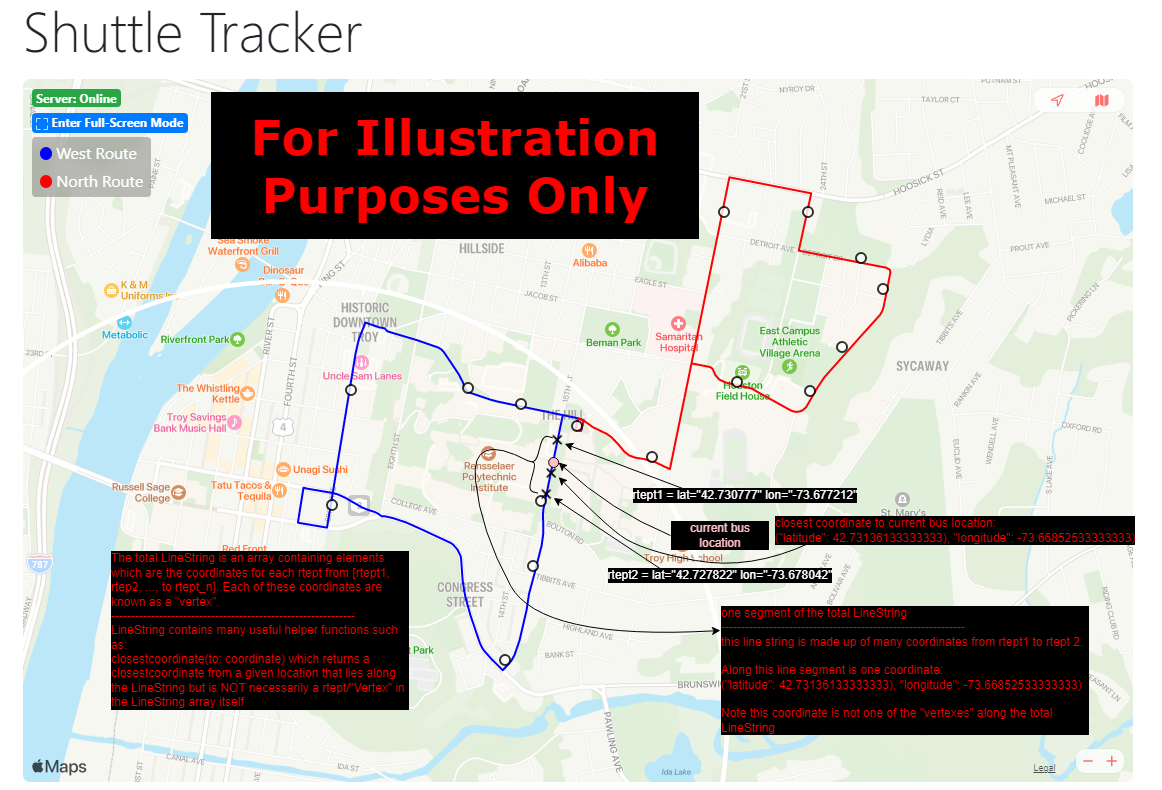
2. Use Turf.js, LineString, to find the closest coordinate along route_m. Note that this closest coordinate may not be a rtept along the route, but instead a coordinate along the LineString from each rtept to the next rtept along route_m.
   • For example in Public > routes-data > fall22.gpx we have:

          <name>West Route</name>
          <cmt>Blue</cmt>
          <rtept lat="42.730777" lon="-73.677212"></rtept>
          <rtept lat="42.727822" lon="-73.678042"></rtept>
          ...

Here is how to interpret the data shown above:

• There exists a route called "West Route"
• one rtept along the route, "West Route", is a rtept with latitude="42.730777" and longitude="-73.677212" which we may refer to as "vertex" in the code.
• a closest coordinate along the LineString may be ("latitude": 42.73136133333333), "longitude": -73.66852533333333). Note that this is NOT a rtept shown in the data above and is furthermore not a rtept that exists at all in the data above if we were to expand the data to show all the rtepts along "West Route".
• the closest coordinate exists in the set of coordinates from one rtept, to another rtept lying along the LineString which is made up of the , <rtept lat="42.727822" lon="-73.678042>, etc...

For illustration purposes only, here is a diagram which outlines some of these key points:

3. Check if the distance between the current bus location to the closest coordinate is within Constants.isOnRouteThreshold
   • true -> return true (implying that the current bus location is on route_m)
   • false -> return false (implying that the current bus location is not on route_m)
4. If (3)
   • true -> has the route segment closest to the bus been set yet? - true -> the bus is on an overlapping route -> return the first route segment - false -> set current route segment to the current route
   • false -> continue to check the next route
   • Note that there might be the same distance to the bus location in the case of overlapping routes. In such an edge case we will return the first route segment.

2. Find the distance along the current route that the bus has traveled from the first rtept to the current bus location

1. Determine the nearest "vertex" to the current bus location. For convenience let us call it rtept 'b'
2. Continuously sum the polyline distances from one rtpet to the next until we reach 'b'
3. At rtept 'b' consider 3 possibles cases in order to get the accurate distance travled
   • 3 Cases:

// If the current rtept is the nearest rtept, determine if the reported bus location is to the left or right of the nearest rtept
// (i.e. Assume we have the following polyline)
//
// |-----|-----| --> |--x1--|--x2--| --> This algorithm determines whether the current bus location, 'x' is either 'x1' or 'x2' relative to the nearest rtept, 'b'
// a     b     c     a      b      c
//
// For brevity assume the following in all polyline cases:
//    Let 'x' be either 'x1' or 'x2' which is determined by the case analysis
//    Let 'a' be the rtept before the nearest rtept in the entire route
//    Let 'b' be the nearest rtept in the entire route
//    Let 'c' be the rtept after the nearest rtept in the entire route
//
// This step is needed in order to determine whether the distance the bus has traveled includes 'a' to 'x1' or instead 'b' to 'x2'
//
// There are 3 cases: 1) distance(a,b) == distance(b,c)
//                    2) distance(a,b) < distance(b,c)
//                    3) distance(a,b) > distance(b,c) 

Case 1)

// Assume the following polyline (for case 1):
// Goal: Given the current bus location, x, determine if x=x1 or if x=x2
//
// |--x1--|--x2--| 
// a      b      c
//
// if distance(a,x) < distance(x,c) then x = x1 which implies the bus has just passed rtept 'a' and that we must sum the remaining distance from 'a' to x==x1
// Otherwise x == x2 which implies the bus has just passed rtept 'b' and that we must sum the remaining distance from 'b' to x==x2

Case 2)

// Assume the following polyline (for case 2):
// Goal: Given the current bus location, x, determine if x=x1 or if x=x2
//
// |--x1--|--x2-------| 
// a      b           c
//
// Suppose we have delta1 < delta2. By direct proof the following is true (for brevity assume distance(...) == d(...)):
// delta1 = d(b,c) - d(a,x)
// delta2 = d(b,c) - d(a,b)
// delta1 < delta2 --> d(b,c) - d(a,x) < d(b,c) - d(a,b) --> -d(a,x) < -d(a,b) --> d(a,x) > d(a,b)
// if delta1 < delta2 then d(a,x) > d(a,b) then x = x2 which implies the bus has just passed rtept 'b' and that we must sum the remaining distance from 'b' to x==x2
// Otherwise x == x1 which implies the bus has just passed rtept 'a' and that we must sum the remaining distance from 'a' to x==x1

Case 3)

// Assume the following polyline (for case 3):
// Goal: Given the current bus location, x, determine if x=x1 or if x=x2
//
// |-------x1--|--x2--| 
// a           b      c
//
// Suppose we have delta1 < delta2. By direct proof the following is true (for brevity assume distance(...) == d(...)):
// delta1 = d(a,b) - d(c,x)
// delta2 = d(a,b) - d(b,c)
// delta1 < delta2 --> d(a,b) - d(c,x) < d(a,b) - d(b,c) --> -d(c,x) < -d(b,c) --> d(c,x) > d(b,c)
// if delta1 < delta2 then d(c,x) > d(b,c) then x = x1 which implies the bus has just passed rtept 'a' and that we must sum the remaining distance from 'a' to x==x1
// Otherwise x == x2 which implies the bus has just passed rtept 'b' and that we must sum the remaining distance from 'b' to x==x2

4. Now we must note that as of 12/08/2022 each route is currently represented as a list of rtepts where the final rtept in the list is not the starting rtept in the list.
   • This means, for example, that if a bus starts at the rtept which represents "the Union", the final rtept in the list is NOT "the Union" but instead a coordinate point that is along the way back to "the Union"
   • Therefore we must determine whether the bus is traveling back to the Union or away from the union to get an accurate distance of how far the bus has actually traveled.
     • Therefore we will ** several key assumptions**
       • 1. The bus has at least two locations points. One location point must be the current bus location. The second location point must be the previous bus location before the current bus location AND the two bus locations cannot be the same.
       • 2. The list of rtepts is the order the bus will begin traversing the route.
   • Our algorithm will look as follows:

// Find the nearest vertex to the current bus location and call it nearestRTEPT
// Find the neraest vertex to the previous bus location and call it oldestPassedRTEPT
//
// Find the index of nearestRTEPT in the LineString of rtepts for the current route and call it currentRTEPTIndex
// Find the index of oldestPassedRTEPT in the LineString of rtepts for the current route and call it previousRTEPTIndex
//
// There are 3 cases: 1) currentRTEPTIndex == previousRTEPTIndex
//                    2) currentRTEPTIndex < previousRTEPTIndex
//                    3) currentRTEPTIndex > previousRTEPTIndex

Case 1)

// There is not enough information to determine which direction the bus is going. Therefore we cannot make any determinations about the distance the bus has actually traveled

Case 2)

// Since the index of the rtept for the current bus location is earlier than the index of the rtept for the previous bus location we may conclude the bus is traveling back to the start of the route
// 
// Therefore the intuition for calculating the distance the bus has traveled is as follows:
// 1) Sum the entire distance of the route from rtept_n to rtept_n+1
// 2) At the nearest vertex we have the following polyline:
//
// |--x1--|--x2--| 
// a      b      c
// <-------------- (Note this is the direction the bus is traveling in this instance)
//
//  Our goal will be to determine if x=x1 or if x=x2. It is important to note here that we will be iterating from a, to b, to c when we enumerate over the rtepts of the route.
//
// Case 1) x = x1
// We will have already enumerated over rtept a, and are now at rtept b
// At rtept b we will add distance(b,x1) because that is the distance the bus has traveled from rtept 'b' to its current location, x1, while enroute to rtept 'a'
//
// Case 2) x = x2
// We will have already enumerated over rtept a, and are now at rtept b
// At rtept b we will add distance(c,x2) because that is the distance the bus has traveled from rtept 'c' to its current location, x2, while enroute to rtept 'b'
//
// Therefore at the nearest vertex we will make the following optimization to avoid iterating over the route twice:
//
// Assume we have the following polyline:
// |--...-x1--|--x2-...--| (The ellipses represent that we may have polyline Case1, Case2, or Case3 from (3) since there is an arbitrarily long distance from 'a' to 'x1' and 'x2' to 'c') 
// a          b          c
// <---------------------- (Note this is the direction the bus is traveling in this instance)
//
// If the direction is reversed then the bus has completed the route and is coming back to the first rtept
// Therefore there are 2 cases:
//      1) The bus is before the nearest rtept, 'b', and 'x' is 'x1'
//      2) The bus is after the nearest rtept, 'b', and 'x' is 'x2'
//
//  Case 1)
//    distanceAlongRoute += dist(a,b) // We must sum the distance the bus took to complete the entire route which includes the rte segment, 'a' to 'b'
//    distanceAlongRoute += dist(b,'x1') // The distance the bus has traveled on its way back from the completion of the route which is 'b' to 'x1'
//
//  Case 2)
//    distanceAlongRoute += dist(b,c) // We must sum the distance the bus took to complete the entire route which includes this rte segment, 'b' to 'c'
//    distanceAlongRoute += dist(c,'x2') // The distance the bus has traveled on its way back from the completion of the route which is 'c' to 'x2'
//
// After adding this distance continue enumerating the remaining rtepts and summing the remaining distances from rtept_n to rtpet_n+1

Case 3)

// Since the index of the rtept for the current bus location is later than the index of the rtept for the previous bus location we may conclude the bus has just started traveling away from the start of the route
//
// Therefore we will simply follow (3) with no changes needed to get the progress of the bus along the route