Graph Data Generator

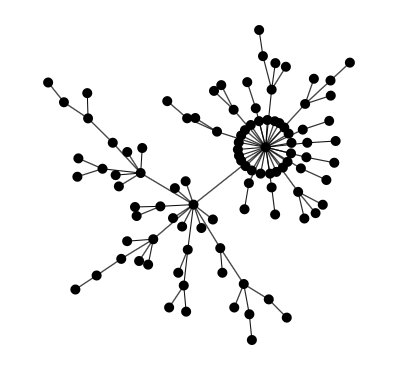
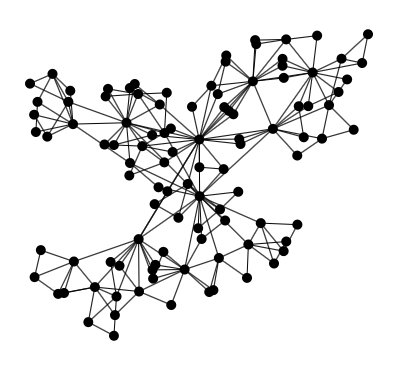
This project generates graphs of arbitrary size using various models. All graphs are reproducible using a seed variable.

Instructions

java -jar out/artifacts/graph_data_generator_main_jar/graph-data-generator_main.jar --help

usage: graph-data-generator
 -b,--dburl <arg>         Database URL
 -d,--directed <arg>      Enable directed edges (boolean)
 -h,--help                Show usage
 -k,--k-value <arg>       Model specific k-value (int)
 -M,--model <arg>         Specify generator model:
                          0 = Barabási–Albert Model (requires -n, -m, -s)
                          1 = Dorogovtsev-Mendes Model (requires -n -s)
                          2 = Erdős–Rényi Model (requires -n, -p, -s, -d)
                          3 = Watts-Strogatz Model (requires -n, -k, -p,
                          -s
 -m,--m-value <arg>       Model specific m-value (int)
 -n,--n-value <arg>       Model specific n-value (int)
 -p,--probability <arg>   Model specific probability (double)
 -s,--seed <arg>          Specify seed value for deterministic
                          reproducibility (int)
 -u,--user <arg>          Database user name

Barabási–Albert Model

Scale-free graph generator using the preferential attachment rule as defined in the Barabási-Albert model.

This is a very simple graph generator that generates a graph using the preferential attachment rule defined in the Barabási-Albert model: nodes are generated one by one, and each time attached by one or more edges other nodes. The other nodes are chosen using a biased random selection giving more chance to a node if it has a high degree.

:Reference: Albert-László Barabási & Réka Albert, Emergence of scaling in random networks, Science 286: 509–512. October 1999. doi:10.1126/science.286.5439.509

Example Usage

java -jar out/artifacts/graph_data_generator_main_jar/graph-data-generator_main.jar --dburl "http://autogenneo4j.sb02.stations.graphenedb.com:24789/" --user someuser --password somepassword --model 0 --n-value 50 --m-value 1 --seed 38498

Dorogovtsev-Mendes Model

Generates a graph using the Dorogovtsev - Mendes algorithm. This starts by creating three nodes and tree edges, making a triangle, and then add one node at a time. Each time a node is added, an edge is chosen randomly and the node is connected to the two extremities of this edge.

This process generates a power-low degree distribution, as nodes that have more edges have more chances to be selected since their edges are more represented in the edge set.

This algorithm often generates graphs that seem more suitable than the simple preferential attachment implemented in the PreferentialAttachmentGenerator class (despite the fact more complex and useful preferential attachment generators could be realized in the future).

The Dorogovtsev - Mendes algorithm always produces planar graphs.

The more this generator is iterated, the more nodes are generated. It can therefore generate trees of any size.

:Reference: S. N. Dorogovtsev and J. F. F. Mendes, Evolution of networks, in Adv. Phys, 2002, 1079–1187

Example Usage

java -jar out/artifacts/graph_data_generator_main_jar/graph-data-generator_main.jar --dburl "http://autogenneo4j.sb02.stations.graphenedb.com:24789/" --user someuser --password somepassword --model 1 --n-value 100 --seed 38498

Erdős–Rényi Model

In the model introduced by Erdős and Rényi, all graphs on a fixed vertex set with a fixed number of edges are equally likely. These models can be used in the probabilistic method to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all graphs.

Example Usage

java -jar out/artifacts/graph_data_generator_main_jar/graph-data-generator_main.jar --dburl "http://autogenneo4j.sb02.stations.graphenedb.com:24789/" --user someuser --password somepassword --model 2 --n-value 100 --probability 0.01 --seed 38498 --directed true

Watts-Strogatz Model

This generator creates small-world graphs of arbitrary size.

This generator is based on the Watts-Strogatz model.

:Reference: Watts, D.J. and Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 393 (6684): 409–10. doi:10.1038/30918. PMID 9623998. 1998.

Example Usage

java -jar out/artifacts/graph_data_generator_main_jar/graph-data-generator_main.jar --dburl "http://autogenneo4j.sb02.stations.graphenedb.com:24789/" --user someuser --password somepassword --model 3 --n-value 100 --k-value 5 --probability 0.3 --seed 38498

Neo4j Storage Details

Node store format

Node records are 15 bytes (* 8 = 120 bits) long:

• 35 bits for first relationship identifier
• 36 bits for first property identifier
• 40 bytes for label field: If there are at most 7 labels attached to the node, and each of label identifiers takes no more than (40 - 4 = 36) / numberOfLabels, i. e. if there are 7 labels, each label id should be below 2(36 / 7) = 5 = 32, than number of labels is stored in 36..38-th bits of the label field, and the label identifiers are packed in lower 0..35-th bits. Otherwise, if there are more than 7 labels attached to the node, or their identifiers are too big, 39-th bit of the label field, i. e. the flag, is set, and in the lower 0..35-th bits of the label field the identifier of the dynamic record with all label ids is stored.
• 9 bits -- some flags and reserved for future use

Relationship store format

Since node keeps only a reference to the single relationship, relationships are orginized in doubly-linked lists, that makes all relationships of some node traversable from this node. Each relationship is a part of two linked lists: a list of relationships of the first node, i. e. from which this relationship starts, and a lists of relationships of the second node, i. e. at which this relationships ends.

Relationship record take 34 bytes (* 8 = 272 bits):

• 35 bits of the first node identifier
• 35 bits of the second node identifier
• 35 * 4 = 140 bits of identifiers of the sibling relationships in two linked lists, this relationship participate in
• 16 bits of relationship type
• 36 bits for first property identifier
• 10 bits -- some flags and reserved for future use

Organazing relationships in linked lists is not particularly performant decision itself, but in some cases it becomes really disastrous -- for example, when some type of nodes has (on average) 100 relationships of type A and some relationships of type B. If we are only interested in traversal over relationships of type B, and they are occasionally clustered in the end of linked lists of the nodes of our type, we are required to traverse 100 relationships in which we are not currently interested to access the useful data.

Apparently to optimize cases like explained above, Neo4j supports another relationship layout (called dense node), in a nutshell it links relationships of each node in a tree, rather than simple linked list. In this case, "first relationship identifier" is interpreted as an identifier of a relationship group. Each relationship group is dedicated to relationships of a certain type. Relationship group record is 25 bytes (* 8 = 200 bits) long:

• 35 bytes of the node identifier this relationship group belongs to
• 16 bits of relationship type
• 35 bytes of the first out relationship identifier, i. e. a relationship which has the given type and starts in the node owning this relationship group
• 35 bytes of the first in relationship identifier, i. e. a relationship which has the given type and ends in the node owning this relationship group
• 35 bytes of the first loop relationship identifier.
• 35 bytes of the next linked relationship group of the owning node, i. e. relationship groups form a singly-linked list
• 1 bit for presence flag

One more byte (8 bits) apparently reserved for future use, however I'm not sure, because seems that it would be nicer to fit 24 bytes for relationship group record, because it is more "power of 2 aligned", i. e. plays better with cache lines, pages. When relationship groups are used, relationships of any specified type and direction, could be traversed from from the node with much lesser overhead, skipping potentially a lot of relationships of the node we are not interested in during this traversal.

There is an interesting small optimization: when the node is dense, first relationship records in the doubly-linked lists, to which relationship groups point, keep the length of the doubly-linked list in place of previous relationship link, which is otherwise unused (because first relationship in the doubly-linked list point only to the next relationship in a chain).

Property store format

As nodes and relationships reference only the first their property, they are also stored as doubly-linked lists, by owning primitive entity. Property record size is 41 bytes:

• 36 bits of the previous linked property identifier
• 36 bits of the next linked property identifier
• 32 bytes of "payload", i. e. space where the property data itself is stored. It includes property type identifier, data encoding type and the data bytes. If the property data doesn't fit the payload (i. e. it is a long string or array), the identifier of the linked dynamic data record is placed there as well.

Neo4j supports plenty of property data formats, trying to pack the data as dense as possible, but it is not the subject of this blog post.

References

Erdős–Rényi model, https://en.wikipedia.org/wiki/Erd%C5%91s%E2%80%93R%C3%A9nyi_model

Overview of Generators, http://graphstream-project.org/doc/Generators/Overview-of-generators

Neo4j architecture, http://key-value-stories.blogspot.com/2015/02/neo4j-architecture.html