A Levenshtein automoton contains a pattern string (p) and a Levenshtein edit distance (d). Any input string that matches pattern string within the edit distance will report a match. A pattern string is used to populate the Levenshtein automaton STE's with characters. The edit distance is the number of edits - insert, substitute, or delete - that are allowed in any matchine string. Levenshtein automata are used to find closely matching strings, for instance a spell checker could use a Levenshtein automata to look for cloesly matching words for a misspelled word.
Example:
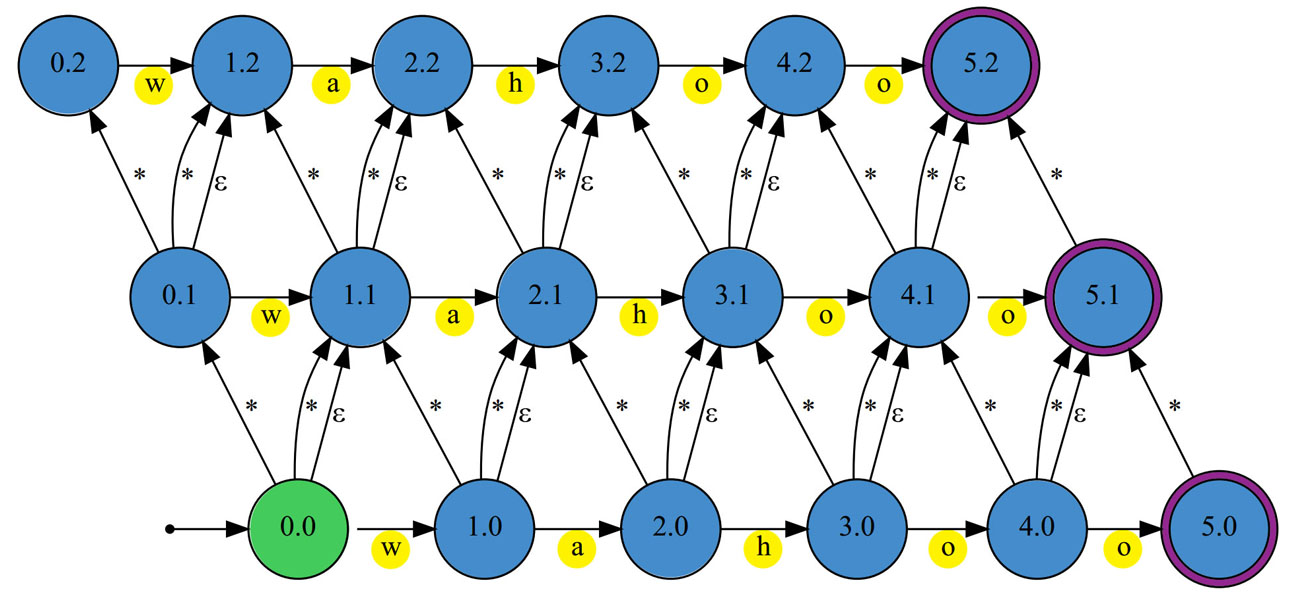
Let's say the given string pattern is s="wahoo" and the Levenshtein edit distance is d=2. A Levenshtein automaton with this pattern and edit distance would look like Figure 1 below. The first number in each state's name is the column number, from zero to the number of characters; for "wahoo" this would be 0-5. The second number is number of edits, from 0 to the edit distance; for d=2 it would be 0-2.
Figure 1 - Levenshtein automaton with string pattern s="wahoo" and edit distance of d=2.[1]
(Starting/always active state is green and reporting states have purple outlines.)
Starting at the first state, (0.0) we feed in the first character of an input string. If the first character is "w" this would move the state to the right, to (1.0), indicating one character match step and zero edits. If it was a blank space this would move to the state right above, to (0.1), indicating it zero successful character steps and one deletion edit. If it was any other character it would move above and to the right, to (1.1), indicating one character step with one insertion or substitution edit. It would then continue on to examine the second character at the active state, either (1.0), (0.1), or (1.1), and move to the next state depending on if it gets a match(right), deletion(up), or insert/substitution(up and right).
If it reaches any of the states to the far right (any 5.X states) this indicates the input string (p) matches the given pattern string within the given edit distance (d). However, if it reaches the top level of the automaton (any of the X.2 states) and encounters a futher edit this will terminate it's movement through the Levenshtein automata, thus preventing a positive match.
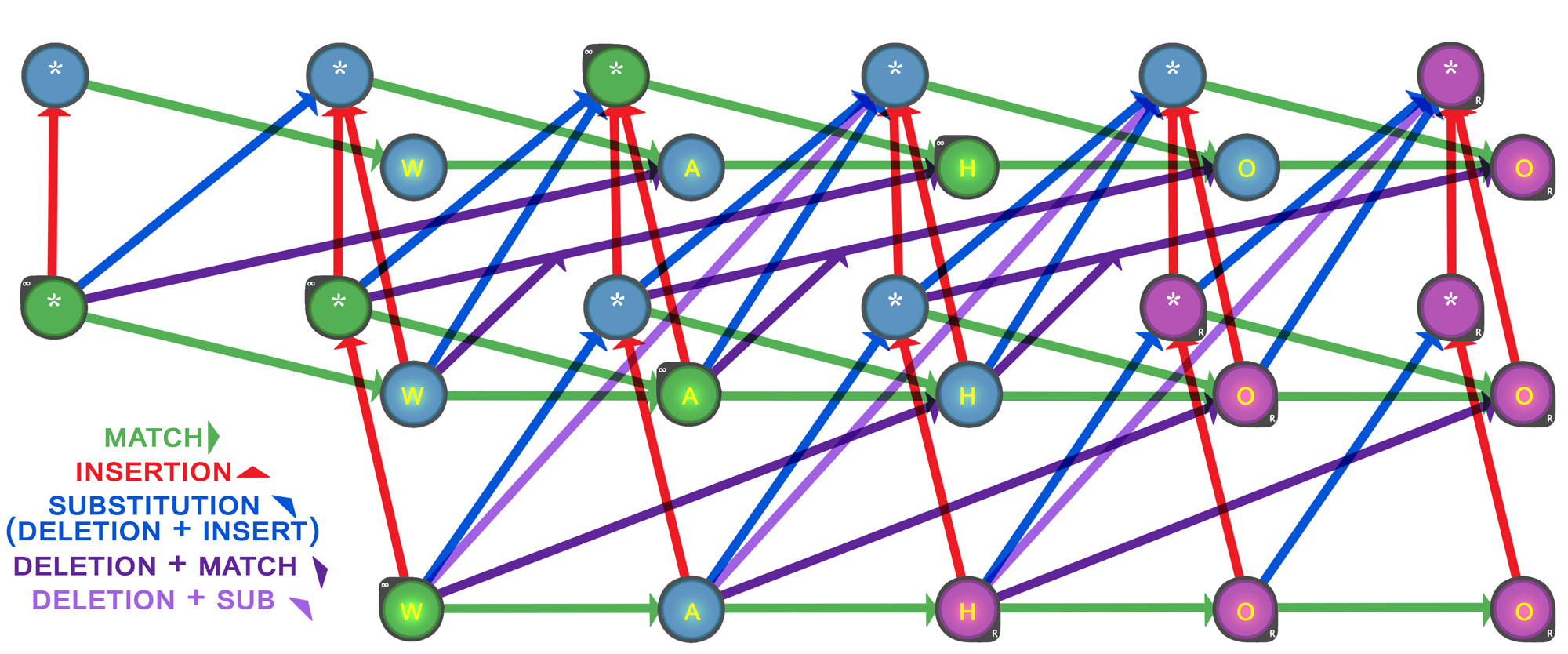
In order to make a Levenshtein automaton using Micron's Automata Processor (AP) we must convert the state machine to an automaton using state transition elements (STE's), which are the single automaton resource units of the AP.
STE's only output a logical yes/no match for the character they are looking for. This means that every output arrow will turn on the attached STE if it finds a match. This also means that extra STE's must be used to simulate the behavior of the automaton. These extra STE's, ( * ), will match on any input and connecting them as shown below in Figure 2 allow us to construct a Levenstein automaton using STE's that has the same behavior as the one above using states in Figure 1.
Figure 2 - Levenshtein automaton built with STE's for the Automata Processor(AP)
(Starting/always active STE's are green and reporting STE's are purple.)
The leven program will accept a string or file of strings as input patterns and create Levenshtein automata with an edit distance chosen by the user. It can also create automatons with random patterns of DNA characters or alpha-numeric characters with a pattern width and edit distance chosen by the user. It will then create an automata network markup language (ANML) file, which is an XML file using the ANML syntax created by Micron.
(See README file in the Code folder for more information on input syntax and program behavior.)
The leven program is dependant on VASim by Jack Wadden from University of Virginia. You will need to download VASim and place it in one folder up when compiling main.cpp (or edit the make file).
[1] T. Tracy et al., "Nondeterministic Finite Automata in Hardware - the Case of the Levenshtein Automaton" University of Verginia, Charlottesville, VA, 2016.