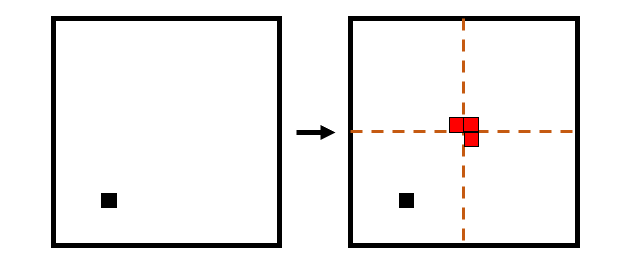
Given a 2^N x 2^N square grid, with a single 1 x 1 square removed, show that it is always possible to tile the remainder of this grid with "L-triominoes" (three squares connected in an "L" shape), regardless of the location of the removed square.
Before revealing the solution, I find that it helps to encourage students to first play around with the setup of the problem and explore possible solutions on their own. I coded an app in Java that allows students to easily and interactively try out different strategies (I also had physical cardboard cutouts of the L tiles which I made myself, though this digital app is more fun, in my opinion).
A Java Runtime Environment of 8 or higher is needed in order to run this app. Try it out for yourself!
The proof is through a clever inductive argument.
Divide the 2^N x 2^N square into four quadrants, each 2^(N-1) x 2^(N-1) in size. Now, the hole must be in one of these quadrants. Place an L at the center, where the four quadrants meet, such that we place one square in every quadrant that doesn't have the hole. Notice then that we have four recursive subproblems---each a 2^(N-1) x 2^(N-1) grid to tile with one square missing somewhere---that we can inductively apply this same strategy to. We eventually hit our base case at N=1, which is clearly tile-able.
The fun thing about the above proof is that it actually allows us to construct what such a tiling would look like.
If we were interested in rendering an image of this final answer, we would necessarily have to assign colors to each of the Ls somehow. Let's impose the restriction that we wish to color the Ls in such a way that no two Ls of the same color will share an edge (though they can touch at corners). This way, even without borders and only using solid colors, we will be able to clearly distinguish the pieces from one another in the solution. Can we find a neat way to color the Ls?
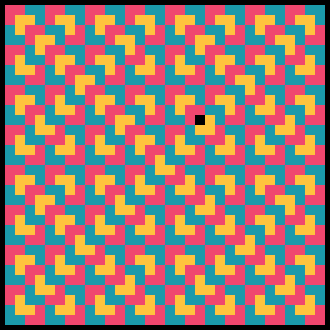
It turns out that yes, there is a very neat way to color the grid, and we can do so using just three colors. We will define two different types of Ls.
In the case where n > 1, let the L which we place at the center be called an inside piece. Clearly no two inside pieces are touching, so we can assign the same color to all of the inside pieces.
In the case where n = 1, let the L which we place be called a base piece. Observe that if we divide the original large 2^N x 2^N grid into a checkerboard of 2 x 2 squares, then we end up with one base piece in each of these squares. So, we can use two more colors, and assign them to the base pieces in a checkerboard pattern.
The above explanation is probably best seen through an image. Fortunately, the images produced by this tiling and coloring are incredibly pretty!
I wrote a Python script which automatically generates png images of the solutions to this problem, given N, the location of the hole, the size of a 1 x 1 square (in pixels), and the three colors to be used in the coloring. I tried out several other color palettes and put them in visuals-maker/samples/ as well. Check them out! I'll show some highlights.
Here are some different colorings to a solution of a 2^5 x 2^5 case.
Here is a coloring to a solution of a 2^6 x 2^6 case.
My script is also capable of creating animated gifs which show the Ls being placed one by one on the board. I think it's quite mesmerizing to watch!
Here's an animated tiling of a 2^4 x 2^4 case.
Now, a 2^5 x 2^5 case,
And finally, a 2^6 x 2^6 case!
As a caveat for anyone interested in using the script for themselves, the method I've come up with is horribly inefficient. It generates a png of each frame using PIL, then uses imageio to stitch them together into a gif. The problem with this is that the filesize can be hilariously large (131 MB for the 2^6 x 2^6 case). Since there are only a handful of pixels different between frames, I was able to use an external website for compressing gifs to bring down the filesize to only 76 kB.
I hope you found this mini-project of mine interesting! I hope to use these resources when bringing this problem to students in the classroom, in the hopes that I convey some sense of the "aesthetic" appreciation of mathematics. Others are welcome to do the same, and I would love to hear how it goes!