AI toy problem test

100% of this code was generated on anthropic's Claude Opus 4.5. Chat transcript here (not including the chats to generate this README or generate_all.sh). All input examples other than "joe_fun" were automatically generated.

Spirograph Generator

A modular system for creating complex mathematical art through composed transformations. Think of it as a digital spirograph toy, but one where you can stack multiple effects on top of each other to create patterns that would be impossible with physical tools.

What Is This?

This tool generates SVG and PNG images of mathematical curves. At its core, it works like the classic Spirograph toy—gears rolling inside gears—but extends far beyond that with:

• Multiple pattern generators: spirograph gears, harmonographs (pendulum simulators), Lissajous curves, roses, polygons, and more
• Transformations you can stack: rotate the whole drawing, slide it along a path, bend straight lines into arcs
• Moiré effects: draw the same pattern multiple times with slight shifts to create interference patterns

Installation

Requirements

• Python 3.8+
• NumPy

Setup

# Clone the repository
git clone https://github.com/foozleface/spirograph-2.git
cd spirograph-2

# Install dependencies
pip install numpy

# Optional: for PNG output
pip install cairosvg

Quick Start

# Generate a simple spirograph
python main.py examples/spirograph_gear_simple.ini

# Generate with PNG output
python main.py examples/harmonograph_simple.ini --png output.png

# Generate all examples
./generate_all.sh --output-dir ./output

The Big Idea: Composed Transformations

The power of this system comes from stacking modules in a pipeline. Each module either generates a pattern or transforms one, and you chain them together to build complexity.

How the Pipeline Works

Every configuration file has a [pipeline] section that lists modules in order:

[pipeline]
modules = spirograph_gear, rotation, arc

This reads as: "Generate a spirograph pattern, then rotate it while drawing, then slide it along an arc path."

The output of each module feeds into the next. A simple gear pattern becomes something entirely different when you add rotation:

Single Module	Two Modules Composed
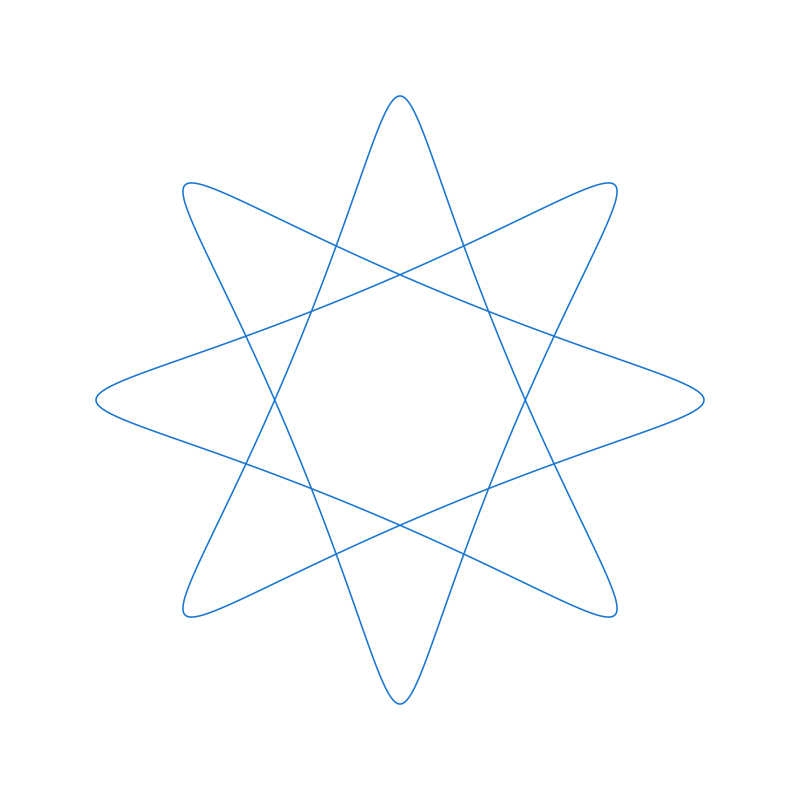modules = spirograph_gear	modules = spirograph_gear, rotation

Additive Complexity

Each module you add creates exponentially more interesting results:

One module — a basic shape:

modules = circle

Two modules — the shape follows a path or transforms:

modules = circle, rotation

Three+ modules — compositions create intricate results:

Multiple modules composed together create organic, intricate patterns

Module Types

Generators (Create Patterns)

Module	Description	Example
spirograph_gear	Classic two-gear spirograph
harmonograph	Pendulum drawing simulator
lissajous	Figure-8s and pretzel curves
rose	Flower petal patterns
polygon	Regular polygons
star_shape	Pointed stars
spiral_shape	Archimedean spirals
line	Lines with timing control

Transforms (Modify Patterns)

Module	What It Does
rotation	Spins the entire pattern around a point while drawing
translation	Slides the pattern along a straight line
arc	Slides the pattern along a circular arc
bend	Warps a straight pattern into a curve (X becomes angle, Y becomes radius)
spiral_arc	Slides along a spiral path

Interesting Examples

Harmonograph: Simulating Pendulums

The harmonograph module simulates a 19th-century drawing machine that uses swinging pendulums. By combining 2-4 pendulums with slightly different frequencies, you get organic, almost hand-drawn looking curves.

Simple	Complex	With Decay

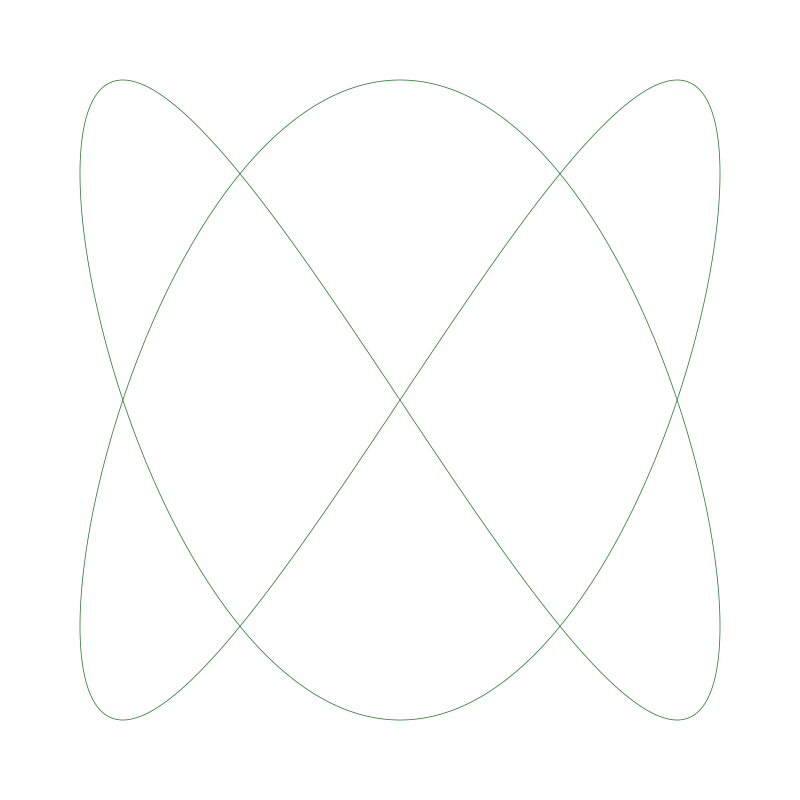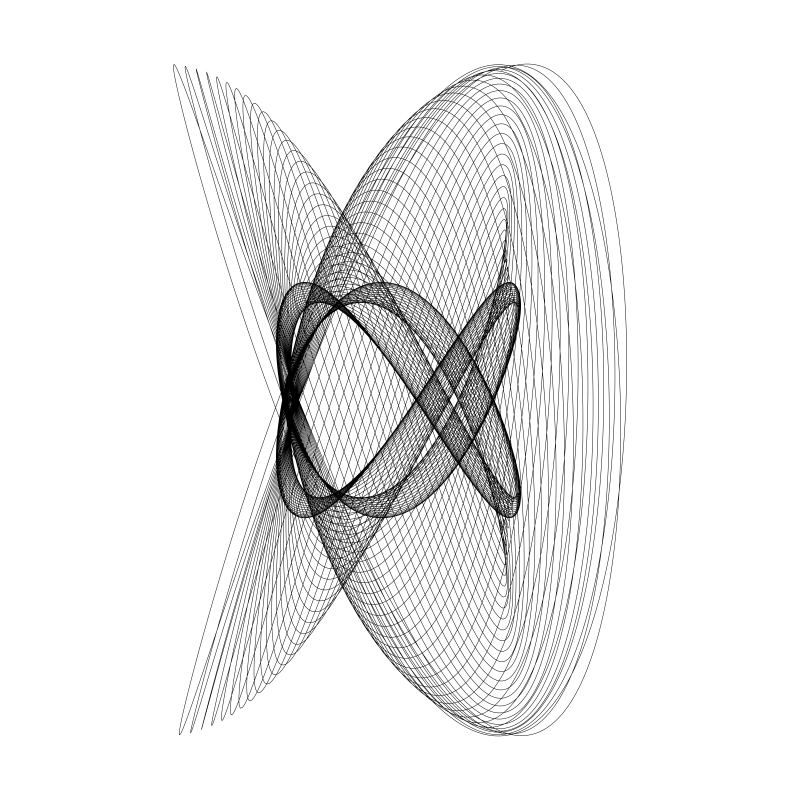[harmonograph]
type = harmonograph
freq1 = 3.0      # X pendulum frequency
freq2 = 2.0      # Y pendulum frequency  
phase2 = 90.0    # Phase offset creates the "opening"
decay1 = 0.01    # Gradual fade-out like real friction

The decay parameter simulates friction—the pattern spirals inward as the pendulums slow down.

Moiré Effects with Cycles

Setting cycles greater than 1 redraws the pattern multiple times. Combined with rotation, this creates moiré interference patterns:

Without Moiré	With Moiré (cycles=8)

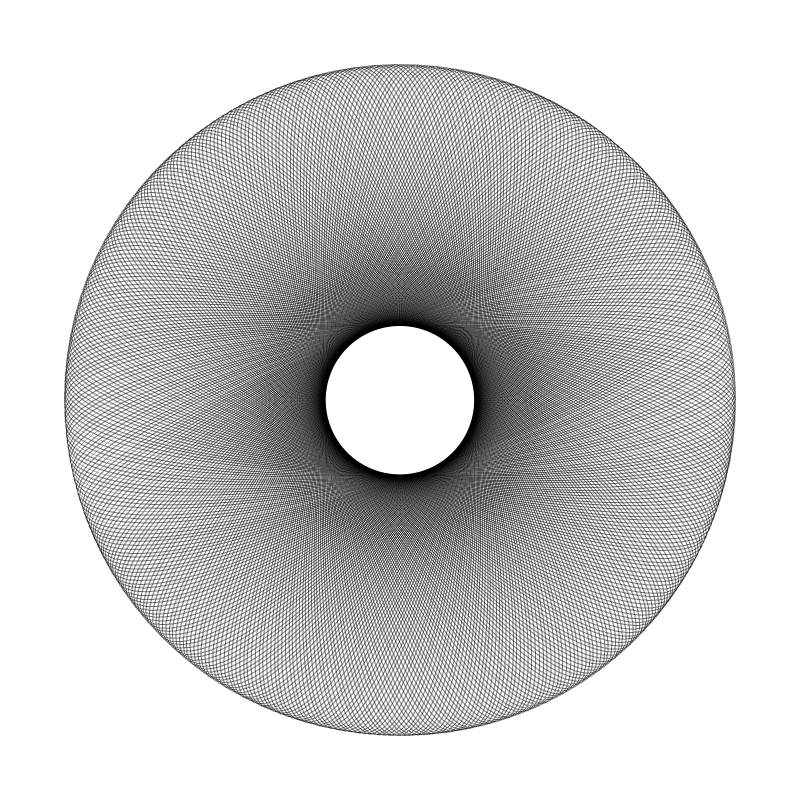[spirograph_gear]
cycles = 8           # Draw the pattern 8 times

[rotation]
total_degrees = 30   # Spread those 8 copies across 30°

Arc vs Bend: Two Ways to Curve

These two transforms both create curved results, but work very differently:

Arc (Sliding)	Bend (Warping)
Pattern slides along a curved path	Pattern itself is bent into a curve

Arc: The pattern keeps its shape but follows a curved trajectory. Like carrying a stamp along a curved rail.

Bend: The pattern's geometry is warped. A straight line becomes a literal arc. X-coordinates become angles, Y-coordinates become radii.

Multiple Rotations

You can apply the same transform multiple times with different parameters:

[pipeline]
modules = gear, rotation_slow, rotation_fast

[rotation_slow]
type = rotation
total_degrees = 30.0

[rotation_fast]
type = rotation
total_degrees = 5.0
origin_x = 50.0  # Different center point

Configuration Reference

Every .ini file has three main sections:

Pipeline

[pipeline]
modules = module1, module2, module3

Output Settings

[output]
filename = my_pattern.svg
width = 800
height = 800
stroke_width = 0.5      # Line thickness
stroke_color = #000000  # Hex color
background_color = #ffffff
margin = 0.1            # 10% margin on each side

Sampling

[sampling]
initial_samples = 100000   # Dense samples for accuracy
output_samples = 10000     # Final point count
use_arc_length = true      # Even spacing along curve

Module Sections

Each module in the pipeline needs its own section with a type parameter:

[my_gear]
type = spirograph_gear
fixed_teeth = 96
rolling_teeth = 36
hole_position = 0.7

[my_rotation]
type = rotation
total_degrees = 45.0

See complete.ini for documentation of every parameter for every module.

Tips for Creating Your Own

1. Start simple: Get one module working, then add transforms one at a time
2. Use cycles for density: cycles = 5 with rotation creates 5 overlapping copies
3. Mind the sampling: Complex patterns need more initial_samples (try 500000+)
4. Thin lines show detail: stroke_width = 0.1 or less for intricate patterns
5. Check the math: Gear teeth ratios determine how many lobes you get. gcd(fixed, rolling) matters.

Gallery

More examples from the compositions:

And from examples:

License

MIT