Problema celor 8 regine este una cunoscută în informatică, care implică aşezarea a 8 regine pe o tabla de şah într-un mod în care nici o regină nu atacă pe celelalte. Pentru a rezolva această problema vom folosi metoda backtracking. În cazul problemei celor 8 regine, backtracking ne permite să încercăm să plasăm reginele pe tabla de şah într-o anumită ordine, iar dacă nu găsim o soluţie, să întoarcem înapoi şi să încercăm altă ordine. Acest proces se repetă până când găsim o soluţie sau epuizăm toate posibilităţile.

Începem prin declararea a doua variabile:

Unde n este o variabilă care memorează dimensiunea tablei de șah, iar R[9] este un vector care memorează pozițiile reginelor pe tabla de șah. R[i] reprezintă coloana în care este plasată regina din i-ul rând. De exemplu, dacă R[3] = 5, înseamnă că regina din al treilea rînd este plasată în a cincea coloană. Dimensiunea vectorului este setată la 9 pentru că dimensiunea maximă a tablei de șah este 8 si vectorul este indexat începand de la 1.

Această funcție verifică daca o poziție dată (x, y) pe tabla de șah este validă pentru a plasa o regină pe tabla de șah n x n. Acest lucru îl face prin iterarea prin rândurile de la 1 la x-1 din tabla de șah si verificând dacă oricare dintre reginele plasate anterior conflictueaza cu poziția (x, y). Dacă este găsit un conflict, funcția incrementează y cu 1 si repetă loop-ul de la primul rand. Dacă y devine mai mare decât n, funcția returnează 0, altfel returnează y. Cele trei verificări din interiorul for loop verifică trei tipuri diferite de conflicte:

• Dacă rândul reginei plasate anterior este același ca rândul poziției care este verificată (R[i] == y).
• Dacă diferența dintre rânduri este aceeași ca diferența dintre coloane (i - R[i] == x - y). Acest lucru ar însemna că reginele sunt pe diagonală.
• Dacă diferența dintre rânduri este aceeași ca diferența dintre coloane (i - x == y - R[i]). Acest lucru ar insemna de asemenea că reginele sunt pe diagonală. Este de menționat faptul că această funcție nu plasează de fapt regina pe tabla de șah, ci doar verifică dacă poziția este validă.

Urmatorul for() loop are blocul de inițializare omis deoarece variabila i este inițializată înafara buclei. 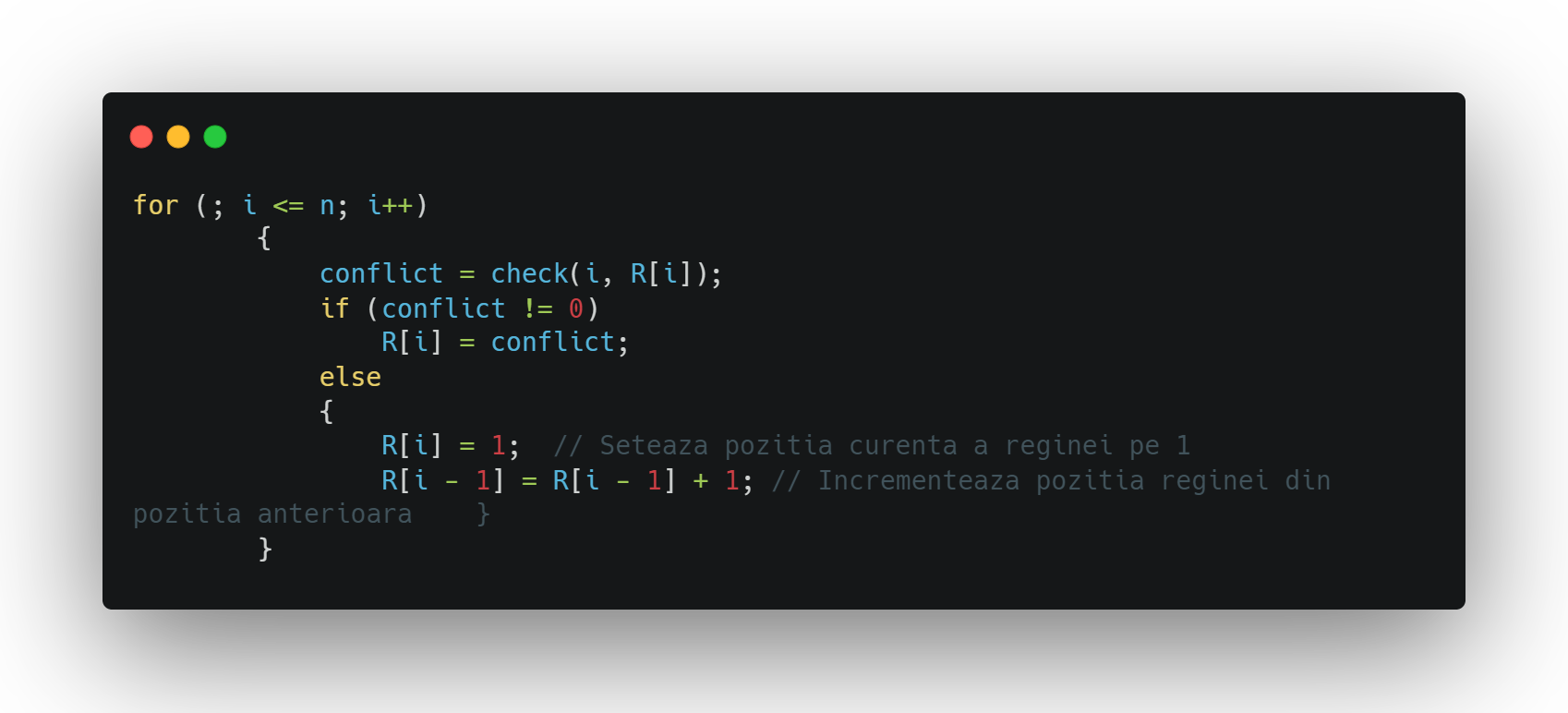Acest for() loop face următoarele:

• Itereaza prin elementele array-ului R de la i la n (i este variabila care ține evidența rândului curent al tablei de șah)

-In interiorul acestui for loop, apelul functiei check() este folosit pentru a verifica dacă poate fi plasată o regină pe poziția curentă. Dacă este posibil să fie plasată o regină, atunci se setează valoarea elementului curent din array-ul R la poziția returnată de funcția check(). Dacă nu este posibil să fie plasată o regină, atunci se face backtracking, adica se seteaza valoarea elementului curent din array-ul R la 1, se incrementeaza valoarea elementului anterior din array-ul R cu 1, și se decrementează valoarea variabilei i cu 2. In acest caz, i este decrementat cu 2 în cazul în care conflict nu este 0. Această decrementare a lui i are ca scop să facă ca bucla să se execute înapoi, cu o poziție, astfel încat să poată verifica dacă există o alta poziție validă pentru regină.

Acești pași sunt repetați până când variabila i depaseste n. Dupa ce variabila i depaseste n, bucla se opreste.

Acest bloc de cod:

face un "nested loop" (bucla aninata) prin care parcurge fiecare poziție a tablei de șah și verifică dacă poziția este ocupată de o regină (R[i]). Daca pozitia este ocupată de o regină, atunci afiseaza "Q", altfel afiseaza "-". Dupa ce se parcurg toate pozițiile de pe aceeași linie, se afișează un rand nou, astfel încat sa se poata afisa intreaga tablă de șah.

La sfârșitul funcției main() avem următoarele linii de cod:

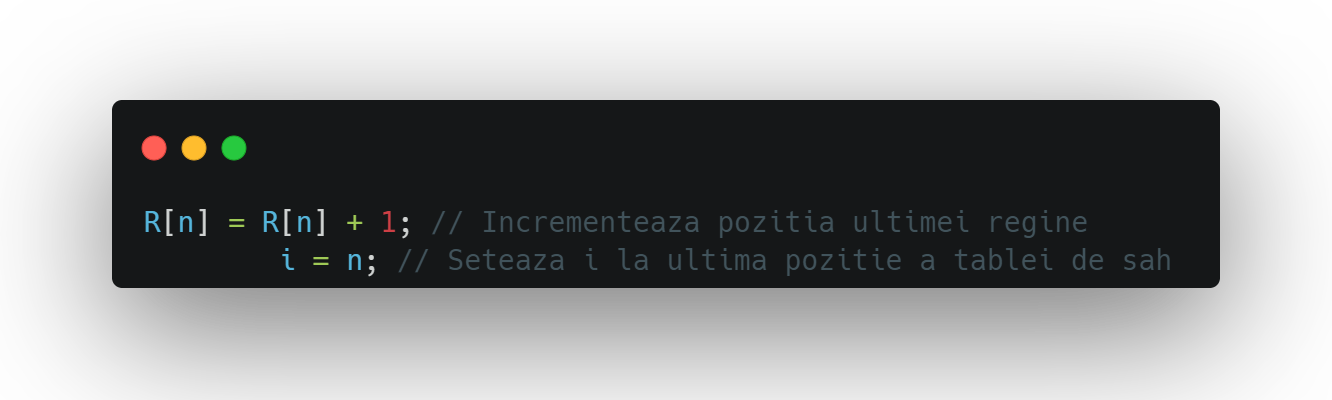
Acest lucru permite ca bucla while să poată fi reluată, începând de la ultima poziție a tablei de șah, verificând dacă există o poziție validă pentru regina în această poziție. Dacă nu există o poziție validă, atunci valoarea lui i va fi decrementată cu 2, asa cum este descris în explicația anterioară, și se va încerca din nou să se plaseze regina pe tabla de șah.

Această problemă se numește "Problema celor 8 Regine" si este o problemă clasică de backtracking. Pentru a rezolva aceasta problema, am folosit metoda de backtracking în care se încercă să se plaseze o regină pe tabla de șah, începand de la prima poziție și mergând spre ultima poziție. Dacă regina poate fi plasata pe o anumită poziție, atunci se trece la urmatoarea poziție și se încerca din nou să se plaseze regină. Dacă regina nu poate fi plasată pe poziția curentă, atunci se face backtracking și se încercă să se plaseze regina pe o altă poziție. Acest proces se repetă până când toate reginele au fost plasate pe tabla de șah, sau pana cand s-a ajuns la o poziție în care nu mai este posibil să se plaseze regina, caz în care se întoarce înapoi la pozițiile anterioare și se încearcă să se găsească o alta poziție validă pentru regină.

În concluzie, rezolvarea acestei problema ajută la dezvoltarea capacităților de viitor programator, deoarece cere folosirea unor metode avansate de programare.