Text-Classification-Naive-Bayes

Naive Bayes-based models to do text classification on IMDB dataset

You can find a sample of dataset in ./data/imdb/

I experiment with three different ways to represent the documents. “Representation” means how you convert the raw text of a document to a feature vector. I use a sparse representation of the feature vectors which is based on a dictionary that maps from the feature name to the feature value.

Document Representations

1. Binary Bag-of-Words: Each document is represented with binary features, one for each token in the vocabulary.

2. Count Bag-of-Words Instead of having a binary feature for each token, I keep count of how many times the token appears in the document, a quantity known as term frequency and denoted tf(d, v).

3. TF-IDF Model The final representation use the TF-IDF score of each token. The TF-IDF score combines how frequently the word appears in the document as well as how infrequently that word appears in the document collection as a whole.

Naive Bayes Experiment

I build three Naive Bayes classifiers, each one using one of the above document representations, and compare their performances on the test dataset.

The prediction rule for Naive Bayes is:

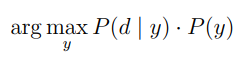
Equations which I implement to build my Naive Bayes classifier:


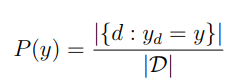
I implement Laplace smoothing on P(v | y) as follows:
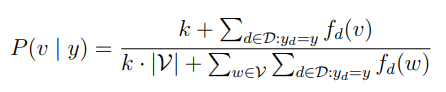where k is a hyperparameter which controls the strength of the smoothing.

The following equation is implemented to make prediction:

Experiment Results

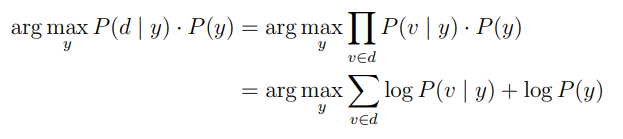
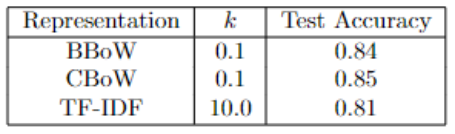
We can see that the most complicated document representation did not get the best results. k helps us in a way that posterior probability does not suddenly drops to zero when there is an additional word not in vocabulary and has p(y|v) = 0. It does this by giving this word a small non-zero probability for both classes. As the value of k goes to infinity, the p(v|y) will go constant value which is 1/|V |.
So, our conditional probability p(v|y) (likelihood) will be very similar. Then, our posterior probabilities p(y|v) will also be similar since posterior = likelihood*prior. I assume priories are very close. Then, our validation accuracies will be around 0.5 for balanced data set for the binary class problem.