注意事项

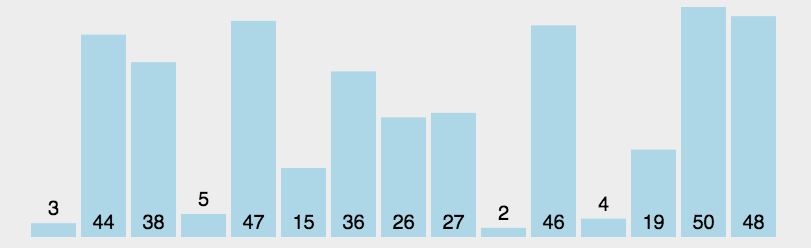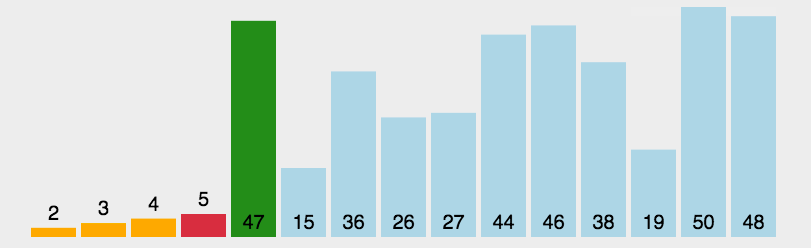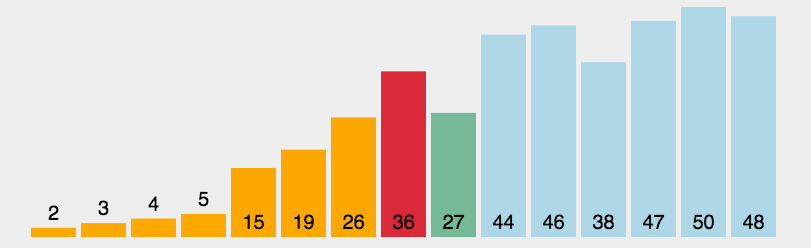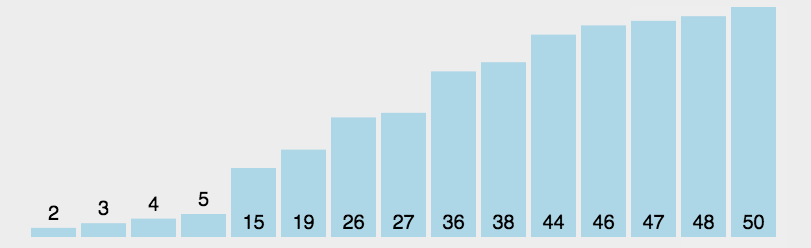
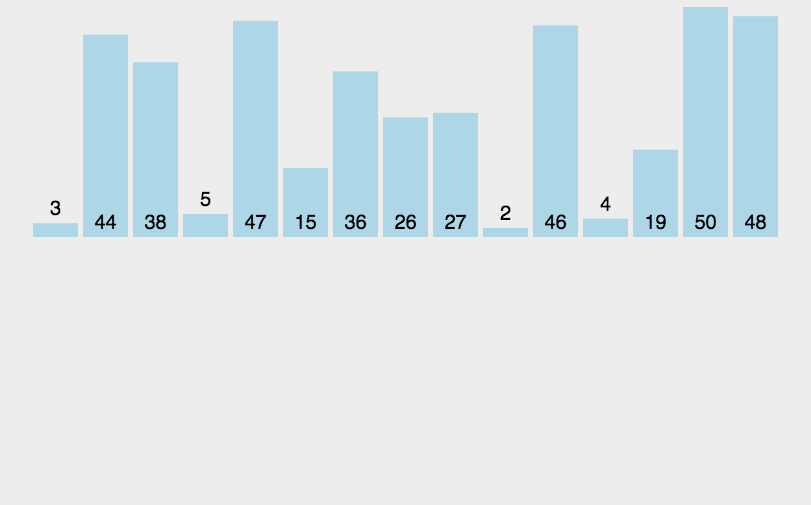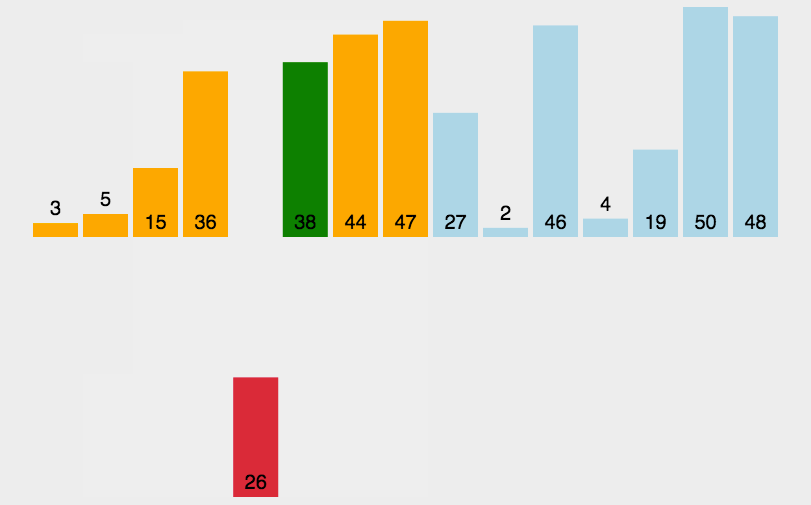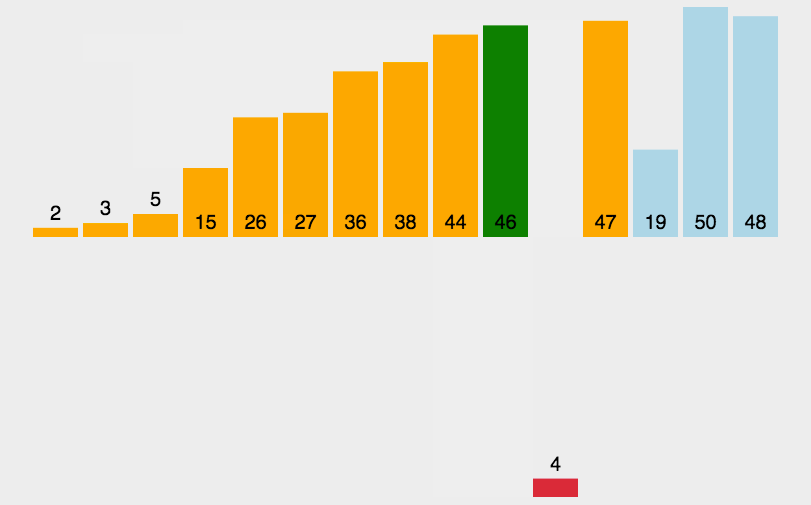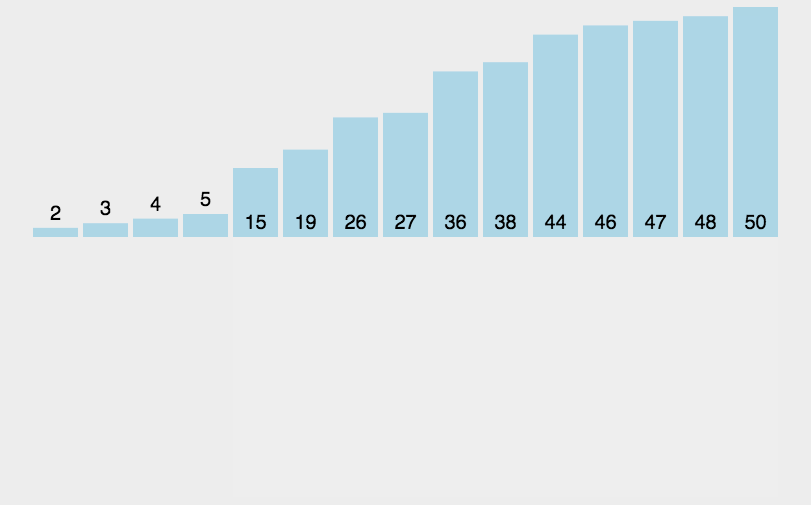
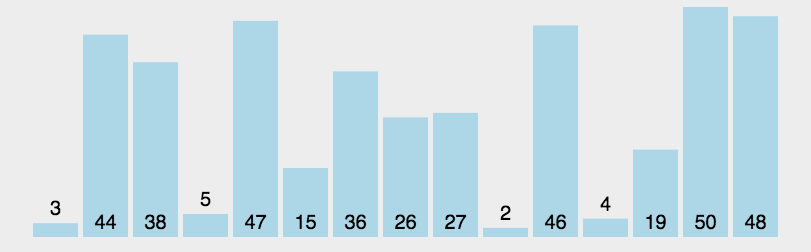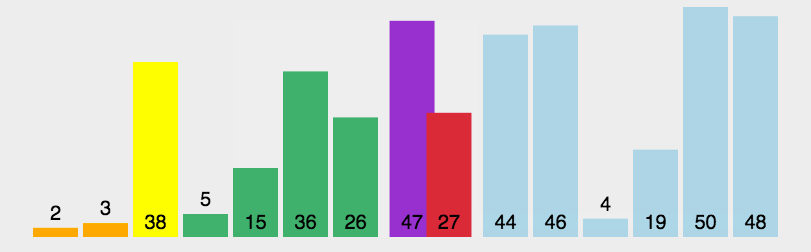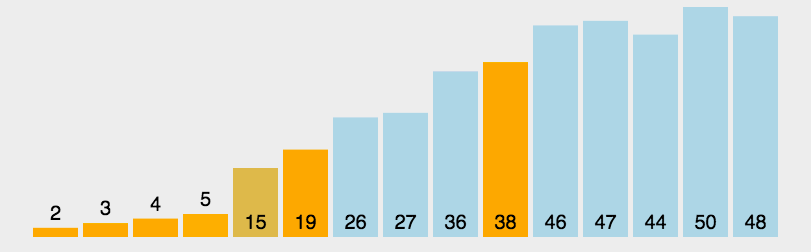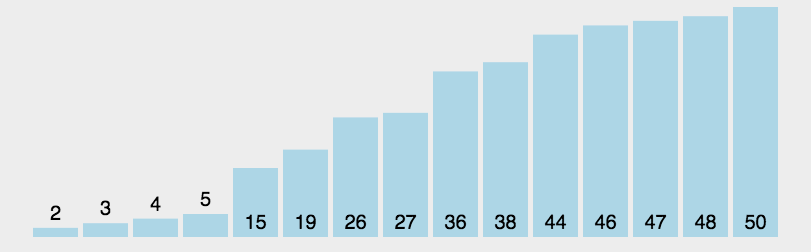
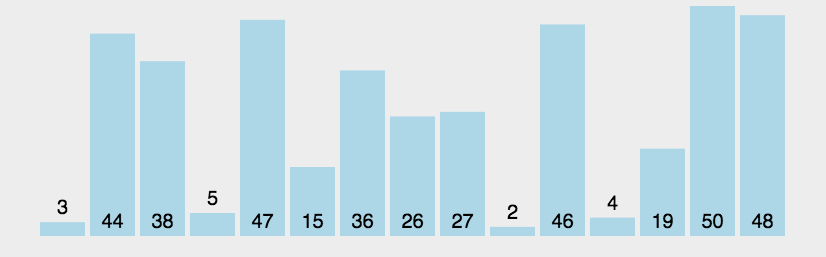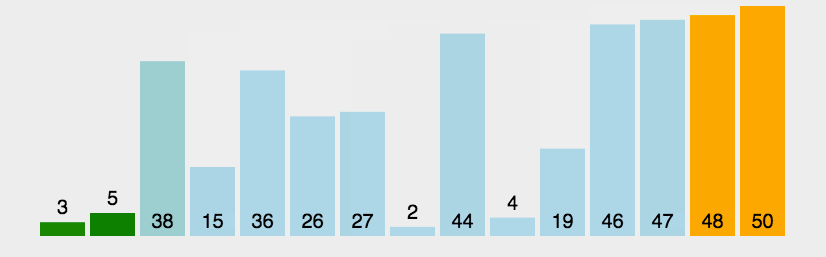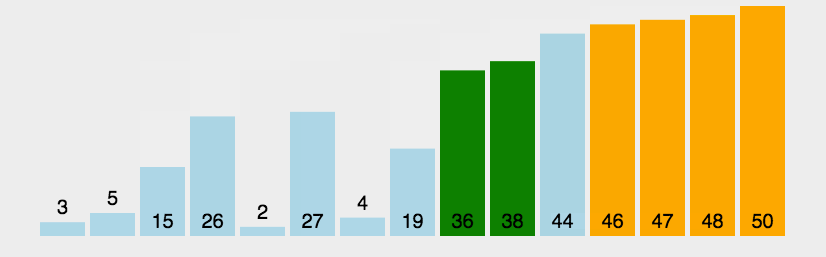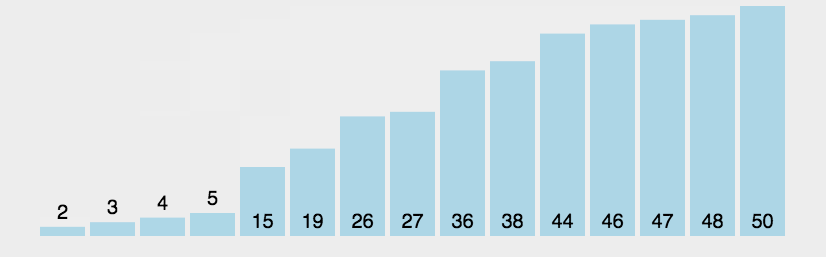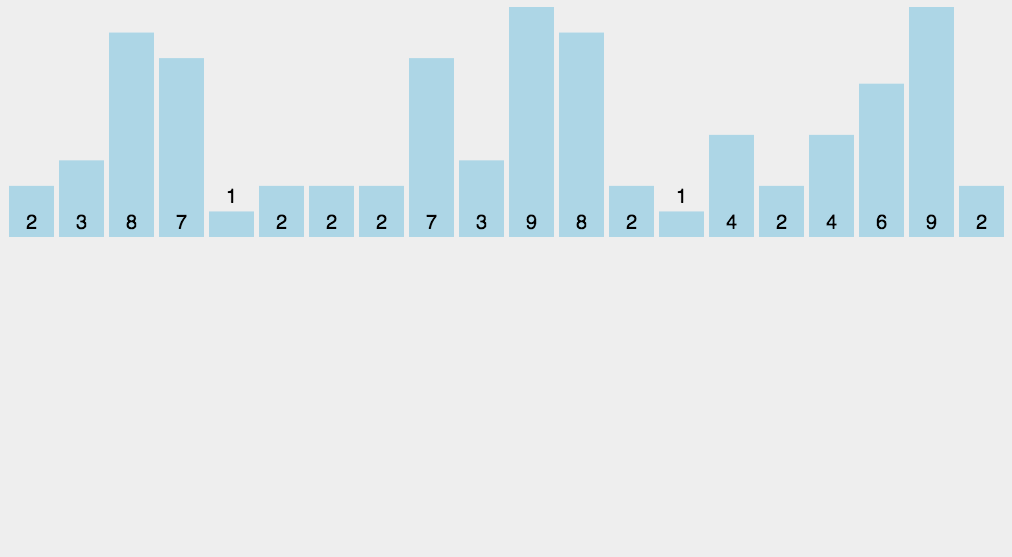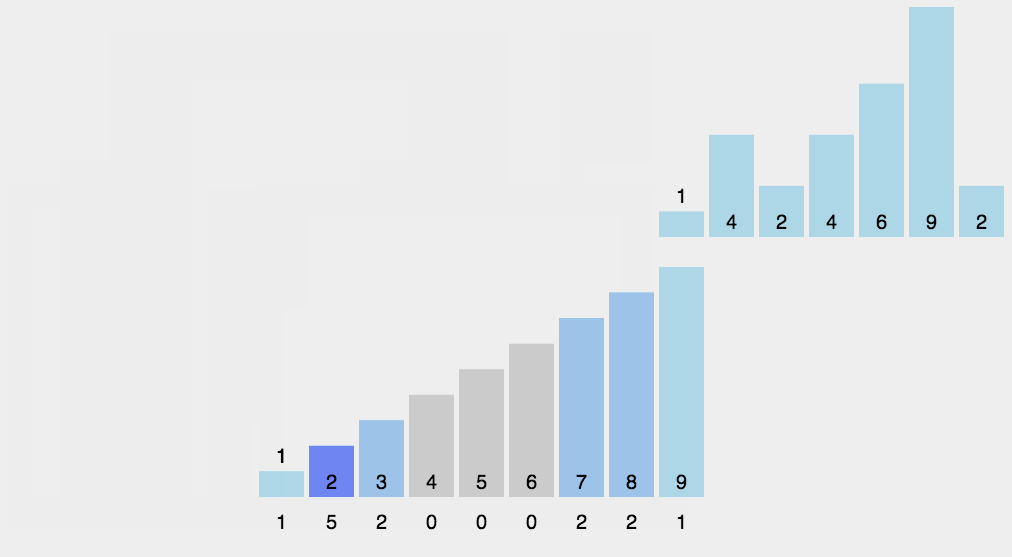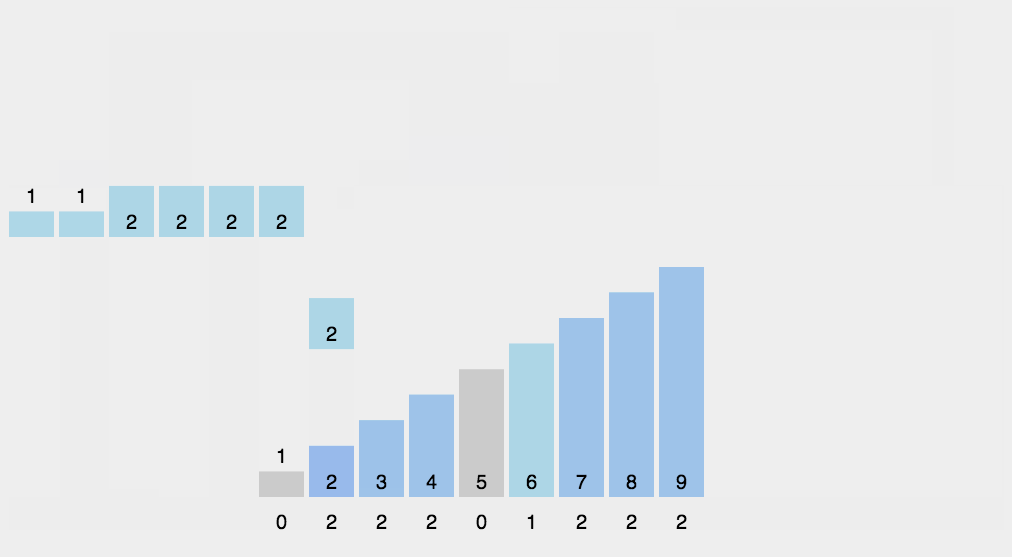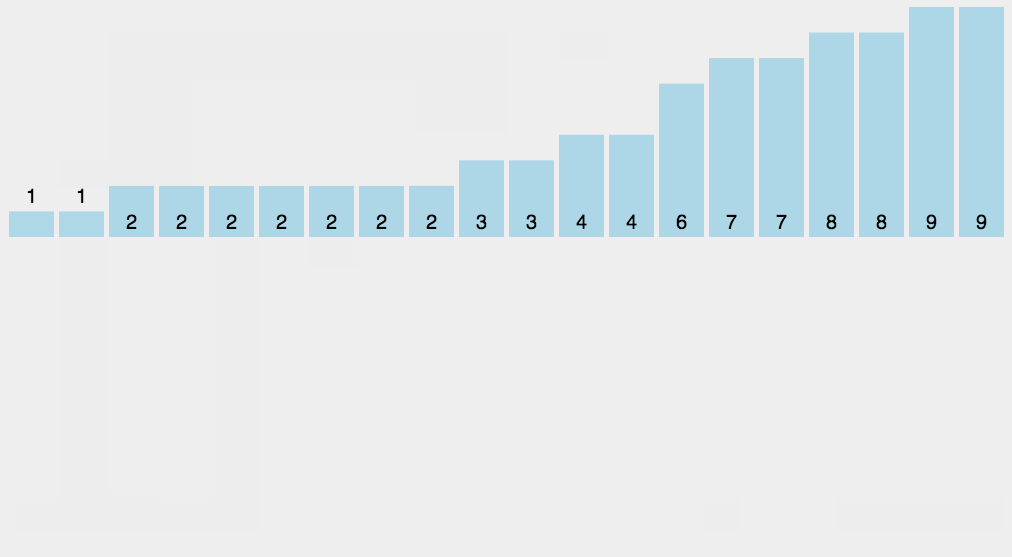概念：

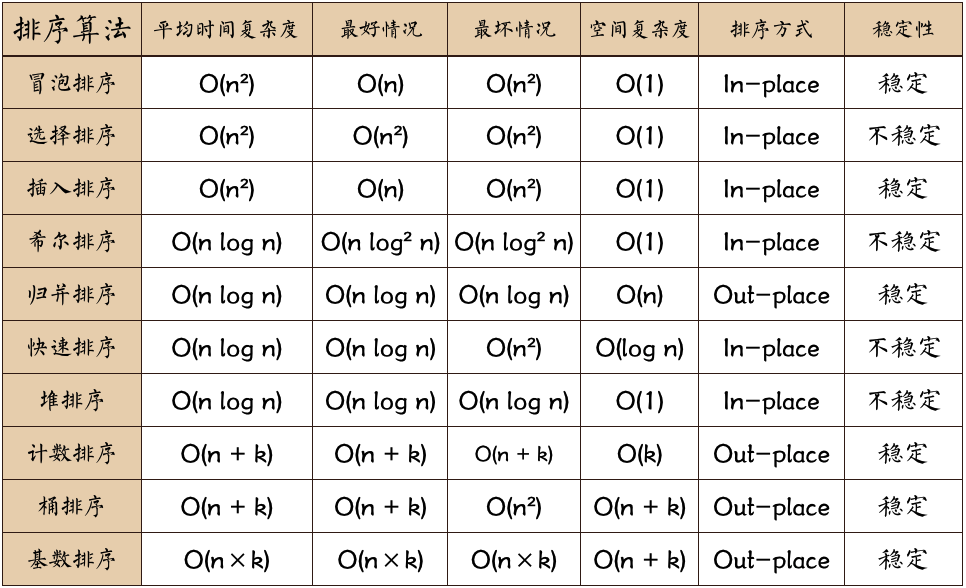
稳定：如果a原本在B前，而a=b，排序之后a仍然在b前 不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。 时间复杂度：对排序数据操作的总次数。反应当n变化时，操作次数呈现什么规律 空间复杂度：是指算法在计算机内执行时所需存储空间的度量，他也是数据规模n的函数

各个方法的各项数据的比较图

各方法的应用总结

(1) 若n较小(n<=100)，可以采用插入和选择排序 当记录规模较小时，直接插入排序较好；否则因为直接选择移动的记录数少于直接插人，应选直接选择排序为宜。 (2) 若数据初始状态基本有序，则选择插入、冒泡和快排 (3) 若n比较大，则采用快排、堆或归并排序 快排是基于内部排序中北认为是最好的方法，当待排序的关键字是随机分布时，快排的平均时间最短； 堆排序的辅助空间少于快速排序， 如果要求稳定可以选择归并排序

0、sort() 排序

定义

使用原型方法，对数组进行排序，并返回数组，默认的顺序是根据字符串Unicode码点。 由于它取决于具体实现，因此无法保证排序的时间和空间复杂性。

代码

arr.sort(compareFunction)        // compareFunction为按照某种顺序进行排列的函数

1、冒泡排序

定义

有时候也叫下沉排序，最简单的也是用的最多的排序方法，它重复的比较相邻的前后二个数据，如果前面的数据大于（或者小于）后面的数据，就将二个数据交换。重复遍历列表，直到全部数组遍历完成。

各项指数

| 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 排序方式 | 稳定性 |

|:---------------:|:------------------:|:---------------:|:--------------:|: -----------:|:--------------:| |O(n²) | O(n) |O(n²)| O(1) | In-place | 稳定 |

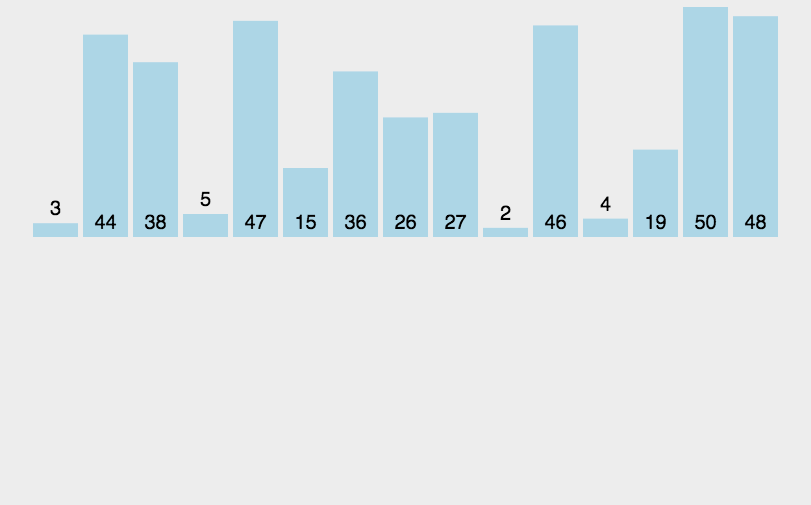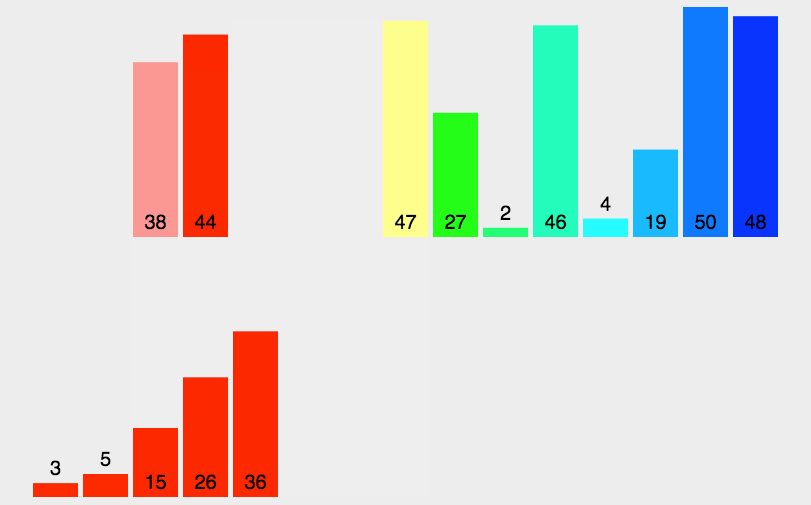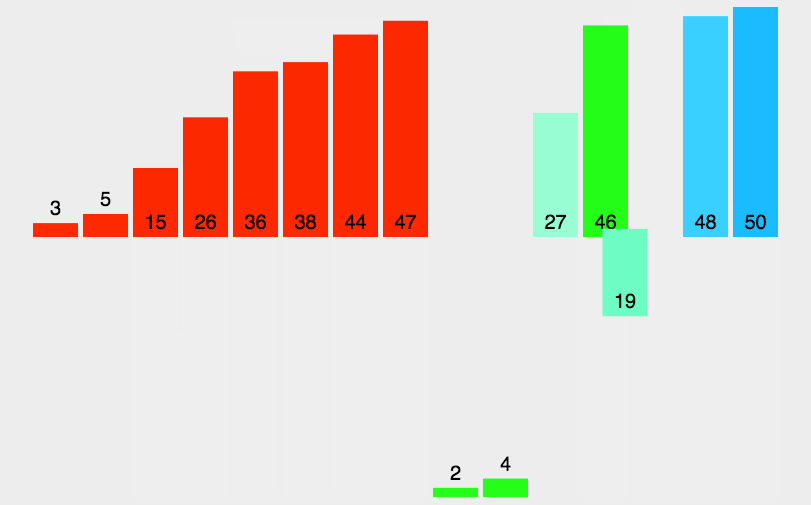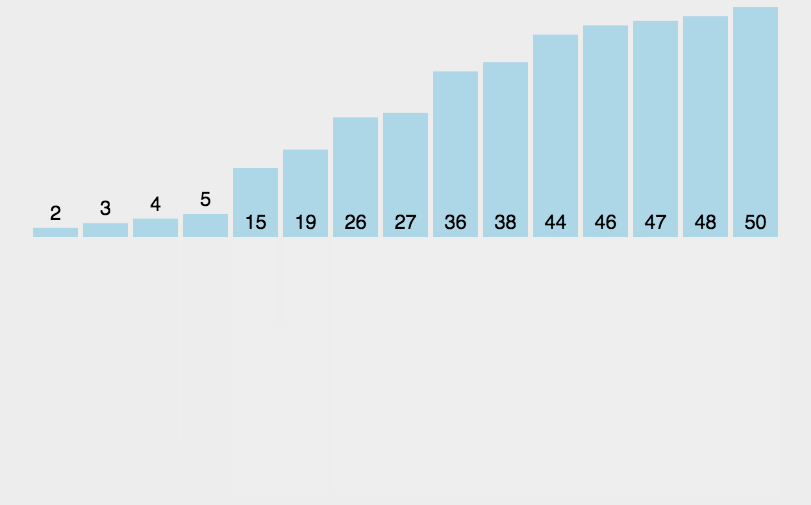
最快：输入的顺序和输出的顺序相同 最慢：输入的顺序和输出的顺序相反 稳定：如果两个数相同的话不会互换位置

应用场景

数据规模小，多用于数字上的比较。

代码

function bubbleSort(arr) {
　　var len = arr.length;
　　for (var i = 0; i < len; i++) {
　　　　for (var j = 0; j < len - 1 - i; j++) {
　　　　　　if (arr[j] > arr[j+1]) { //相邻元素两两对比
　　　　　　　　var temp = arr[j+1]; //元素交换
　　　　　　　　arr[j+1] = arr[j];
　　　　　　　　arr[j] = temp;
　　　　　　}
　　　　}
　　}
　　return arr;
}

以上为最原始的冒泡，可以试着将其改进，比如记录每次遍历最后一次交换的位置（即最大或者最小的位置），下次循环到达此处停止遍历，可以减少时间复杂度。

动图演示

2、选择排序

定义

第一次遍历N个数据，找出其中最小（或最大）的数值与第一个元素交换，第二趟遍历剩下的N-1个数据，找出最小（或最大）的数值与第二个元素交换....一直到第N-1趟。是时间上最稳定的排序算法

各项指数

| 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 排序方式 | 稳定性 | |:---------------:|:------------------:|:---------------:|:--------------:|: -----------:|:--------------:| |O(n²) | O(n²) |O(n²)| O(1) | In-place | 不稳定 |

无论是最好还是最坏都是循环那么多次 不稳定：会交换相同元素的位置

应用场景

数据规模越小越好，最好在少于1000数据的场景中使用。

代码

function selectionSort(arr) {
　　var len = arr.length;
　　var minIndex, temp;
　　for (var i = 0; i < len - 1; i++) {
　　　　minIndex = i;
　　　　for (var j = i + 1; j < len; j++) {
　　　　　　if (arr[j] < arr[minIndex]) { //寻找最小的数
　　　　　　　　minIndex = j; //将最小数的索引保存
　　　　　　}
　　　　}
　　　　temp = arr[i];
　　　　arr[i] = arr[minIndex];
　　　　arr[minIndex] = temp;
　　}
　　return arr;
}

动图演示

3、插入排序

定义

从第i个元素开始，认为该元素以及该元素之前的元素已经被排序，取出第i+1个元素，从第i个元素开始从后往前扫描，如果该元素（已排序）大于新元素，将该元素移到下一位置；重复上一步骤，直到找到已排序的元素小于或者等于新元素的位置；将新元素插入该位置后；再次重复以上操作。(i从0开始) 如果上面不懂可以类比打扑克整理扑克牌的时候的方法。

各项指数

| 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 排序方式 | 稳定性 | |:---------------:|:------------------:|:---------------:|:--------------:|: -----------:|:--------------:| |O(n²) | O(n) |O(n²)| O(1) | In-place | 稳定 |

应用场景

数据量小，而且大部分都已经被排序

代码

function insertionSort(array) {
　　for (var i = 1; i < array.length; i++) {
　　　　var key = array[i];
　　　　var j = i - 1;
　　　　while ( array[j] > key) {
　　　　　　array[j + 1] = array[j];
　　　　　    j--;
　　　　}
　　　　array[j + 1] = key;
　　}
　　return array;
}

动图演示

4、堆排序

定义

利用堆的数据结构设计，堆积是一个近乎完全二叉树的结构，并同时满足堆积的性质；即子节点的键值或索引总是小于（或大于）它的父节点。 创建一个堆，然后将堆首和堆尾切换，把堆缩小1，并且将新数组的数据调整到相应位置。

各项指数

| 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 排序方式 | 稳定性 | |:---------------:|:------------------:|:---------------:|:--------------:|: -----------:|:--------------:| | O(nlog(n)) | O(nlog(n)) | O(nlog(n)) | O(1) | In-place | 不稳定 |

应用场景

适合处理大量数据

代码

var len; // 因为声明的多个函数都需要数据长度，所以把len设置成为全局变量
 
function buildMaxHeap(arr) { // 建立大顶堆
    len = arr.length;
    for (var i = Math.floor(len/2); i >= 0; i--) {
        heapify(arr, i);
    }
}
   
function heapify(arr, i) { // 堆调整
    var left = 2 * i + 1,
    right = 2 * i + 2,
    largest = i;
   
    if (left < len && arr[left] > arr[largest]) {
        largest = left;
    }
   
   if (right < len && arr[right] > arr[largest]) {
        largest = right;
    }
   
    if (largest != i) {
        swap(arr, i, largest);
        heapify(arr, largest);
    }
}
   
function swap(arr, i, j) {
    var temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}
   
function heapSort(arr) {
    buildMaxHeap(arr);
   
    for (var i = arr.length - 1; i > 0; i--) {
        swap(arr, 0, i);
        len--;
        heapify(arr, 0);
    }
    return arr;
}

动图演示

5、归并排序

定义

建立在归并操作上的一种有效的排序算法，分治法。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再将子序列段间有序。 先将长度为n的输入序列分成两个长度为n/2的子序列；再对两个子序列分别采用归并排序，最后将两个排好的子序列合并成一个最终的排序序列

各项指数

| 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 排序方式 | 稳定性 | |:---------------:|:------------------:|:---------------:|:--------------:|: -----------:|:--------------:| | O(nlog(n)) | O(nlog(n)) | O(nlog(n)) | O(n) | Out-place | 稳定 |

应用场景

需要稳定，而空间又不是那么重要的时候。但是js编译器的内存又比较小，很容易造成内存溢出而失败。

代码

function mergeSort(arr) { //采用自上而下的递归方法
　　var len = arr.length;
　　if(len < 2) {
　　　　return arr;
　　}
　　var middle = Math.floor(len / 2),
　　left = arr.slice(0, middle),
　　right = arr.slice(middle);
　　return merge(mergeSort(left), mergeSort(right));
}
 
function merge(left, right){
　　var result = [];
　　while (left.length && right.length) {
　　　　if (left[0] <= right[0]) {
　　　　　　result.push(left.shift());
　　　　} else {
　　　　　　result.push(right.shift());
　　　　}
　　}
 
　　while (left.length){
　　　　result.push(left.shift());
　　}
　　while (right.length){
　　　　result.push(right.shift());
　　}
　　return result;
}

动图演示

6、快速排序

定义

贼拉的快，快的鸡贼。。。 从数列中挑出一个元素，成为基准。遍历数据重新排序数列，所有比基准小的摆放在基准前面，比基准大的摆在基准的后面。在这个分区退出之后，该基准处于数列的中间位置。称为分区操作。最后递归地将小于基准元素的子数列和大于基准元素的子数列排序。

各项指数

| 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 排序方式 | 稳定性 | |:---------------:|:------------------:|:---------------:|:--------------:|: -----------:|:--------------:| | O(nlog(n)) | O(nlog(n)) |O(n²)| O(nlog(n)) | In-place | 不稳定 |

应用场景

数据量大，基本无序时使用。基本有序时使用归并排序。 快排非常脆弱，需要仔细核对。

代码

function quickSort(array, left, right) {
　　console.time('1.快速排序耗时');
　　if (left < right) {
　　　　var x = array[right], i = left - 1, temp;
　　　　for (var j = left; j <= right; j++) {
　　　　　　if (array[j] <= x) {
　　　　　　　　i++;
　　　　　　　　temp = array[i];
　　　　　　　　array[i] = array[j];
　　　　　　　　array[j] = temp;
　　　　　　}
　　　　}
　　　　quickSort(array, left, i - 1);
　　　　quickSort(array, i + 1, right);
　　}
　　console.log(array)
　　return array;
}

动图演示

7、希尔排序

定义

该方法开始于对彼此相距很远的元素对进行排序，然后逐步减少要比较的元素之间的间隙。从相距较远的元素开始，他可以比较简单的最近邻交换更快的将一些异地元素移动到位置。 可以看做是对插入排序的一种优化方法。

各项指数

| 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 排序方式 | 稳定性 | |:---------------:|:------------------:|:---------------:|:--------------:|: -----------:|:--------------:| | O(nlog(n)) |O(nlog²(n))|O(nlog²(n))|O(1) | In-place | 不稳定 |

应用场景

数据量小，而且大部分都没有被排序

代码

function shellSort(arr) {
    var len = arr.length,
    temp,
    gap = 1;
    while (gap < len / 3) { // 动态定义间隔序列
        gap = gap * 3 + 1;
    }
    for (gap; gap > 0; gap = Math.floor(gap / 3)) {
        for (var i = gap; i < len; i++) {
            temp = arr[i];
            for (var j = i-gap; j > 0 && arr[j]> temp; j-=gap) {
                arr[j + gap] = arr[j];
            }
            arr[j + gap] = temp;
        }
    }
    return arr;
}

动图演示

8、计数排序

定义

将数据转化为键值对中的键存储，而他的出现的次数为键值对中的值，但是要求输入的数据必须有确定的范围

各项指数

| 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 排序方式 | 稳定性 | |:---------------:|:------------------:|:---------------:|:--------------:|: -----------:|:--------------:| | O(nlog(n)) |O(nlog²(n))|O(nlog²(n))|O(1) | In-place | 不稳定 |

应用场景

有确定的范围，还可以用作数量多少的排序.

代码

function countingSort(array) {
　　var len = array.length,
　　      B = [],
　　      C = [],
　　      min = max = array[0];
　　for (var i = 0; i < len; i++) {
　　　　min = min <= array[i] ? min : array[i];
　　　　max = max >= array[i] ? max : array[i];
　　　　C[array[i]] = C[array[i]] ? C[array[i]] + 1 : 1;
　　}

　　// 计算排序后的元素下标
　　for (var j = min; j < max; j++) {
　　　　C[j + 1] = (C[j + 1] || 0) + (C[j] || 0);
　　}
　　for (var k = len - 1; k >= 0; k--) {
　　　　B[C[array[k]] - 1] = array[k];
　　　　C[array[k]]--;
　　}
　　return B;
}

动图演示

9、基数排序

定义

基数排序是一种非比较整数的排序方法，他通过将密钥分组为具有相同重要位置和值的各个数字来对整数

各项指数

| 平均时间复杂度 | 最好 | 最坏 | 空间复杂度 | 排序方式 | 稳定性 | |:---------------:|:------------------:|:---------------:|:--------------:|: -----------:|:--------------:| | O(nk) | O(nk) | O(n*k) | O(n+k) | In-place | 稳定 |

k 是最长密钥的长度

应用场景

数据范围小，每个值都要大于0，而且要知道最高位有多少位

代码

function radixSort(arr, maxDigit) {
　　var mod = 10;
　　var dev = 1;
　　var counter = [];
　　for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
　　　　for(var j = 0; j < arr.length; j++) {
　　　　　　var bucket = parseInt((arr[j] % mod) / dev);
　　　　　　if(counter[bucket]== null) {
　　　　　　　　counter[bucket] = [];
　　　　　　}
　　　　counter[bucket].push(arr[j]);
　　　　}
　　　　var pos = 0;
　　　　for(var j = 0; j < counter.length; j++) {
　　　　　　var value = null;
　　　　　　if(counter[j]!=null) {
　　　　　　　　while ((value = counter[j].shift()) != null) {
　　　　　　　　　　arr[pos++] = value;
　　　　　　　　}
　　　　　　}
　　　　}
　　}
　　return arr;
}

动图演示