QuadrilateralFitter

This project is a fork of the original QuadrilateralFitter project. Modifications by Krzysztof Mizgała (2025). Licensed under the MIT License. The original Python code has been rewritten in C to boost performance.

QuadrilateralFitter is an efficient and easy-to-use library for fitting irregular quadrilaterals from polygons or point clouds.

QuadrilateralFitter helps you find that four corners polygon that best approximates your noisy data or detection, so you can apply further processing steps like: perspective correction or pattern matching, without worrying about noise or non-expected vertex.

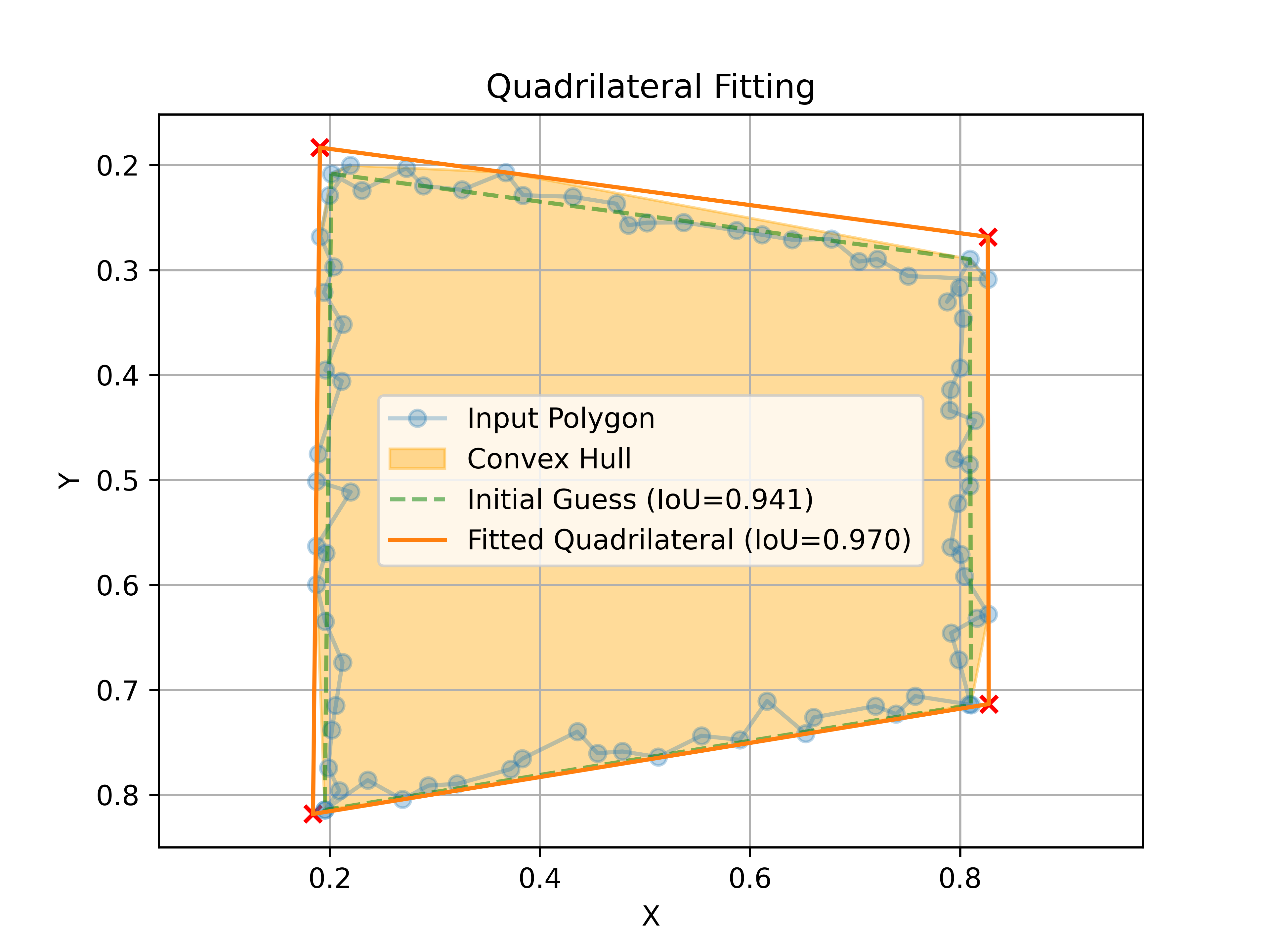
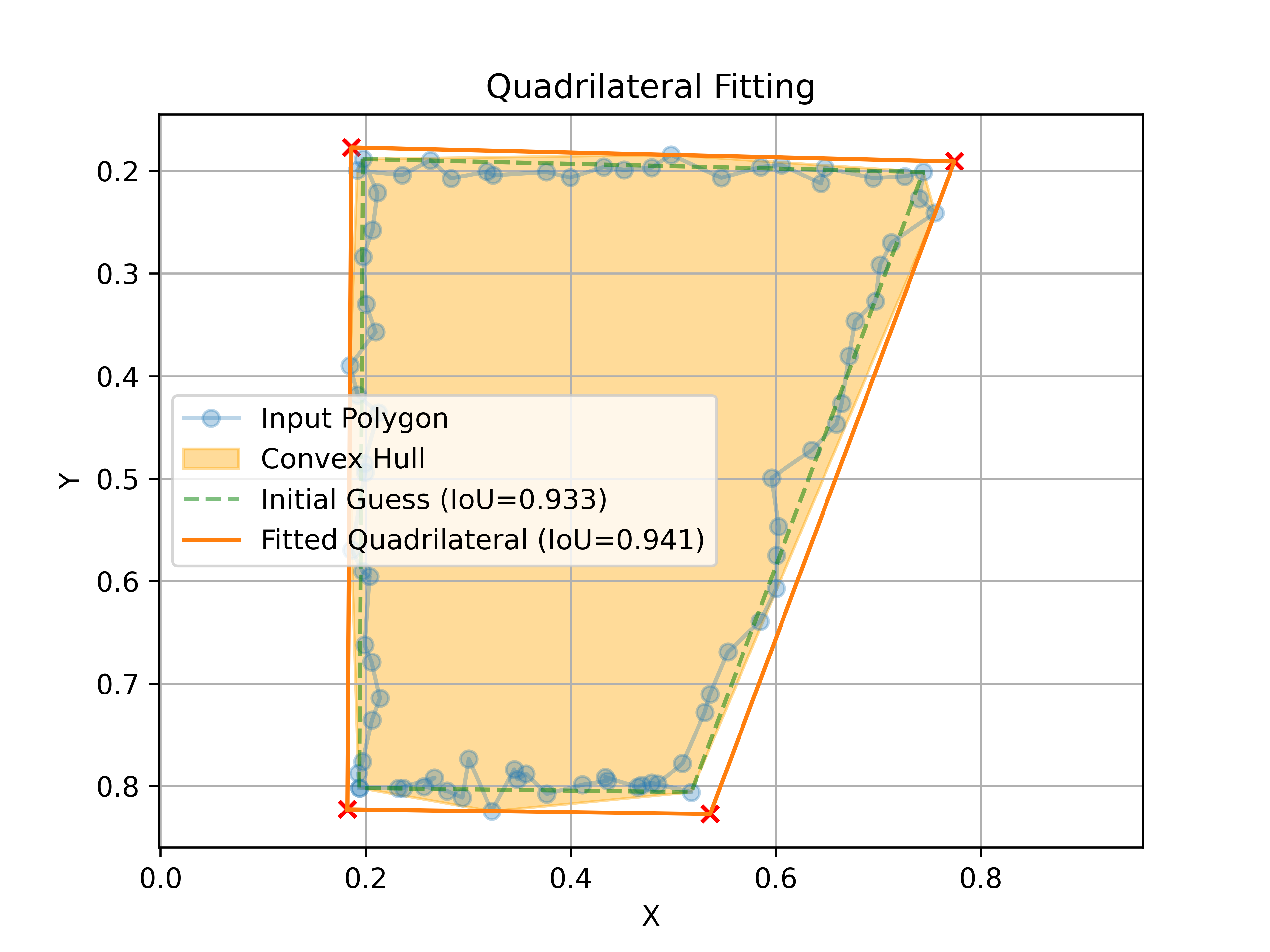
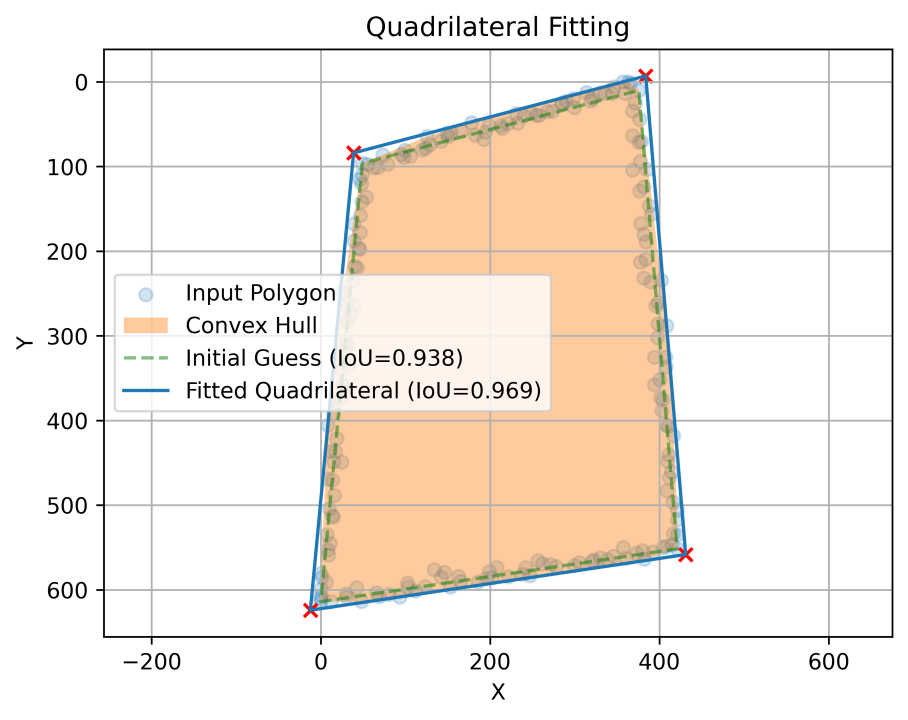
Optimal Fitted Quadrilateral is the smallest area quadrilateral that contains all the points inside a given polygon.

Installation

You can install QuadrilateralFitter with pip:

pip install quadfit

Usage

The simplest way to use QuadrilateralFitter is just one line:

from quadfit import QuadrilateralFitter

# Fit an input polygon of N sides and get the final quadrilateral directly
quad = QuadrilateralFitter(polygon=your_noisy_polygon).fit()

Optionally, you can trade a bit of accuracy for speed and determinism using the additional arguments of fit:

# Limit the number of initial combinations and fix RNG seed; choose stage with 'until'
quad = QuadrilateralFitter(your_noisy_polygon).fit(
  simplify_polygons_larger_than=30,
  start_simplification_epsilon=0.1,
  max_simplification_epsilon=0.5,
  simplification_epsilon_increment=0.02,
  max_initial_combinations=1000,
  random_seed=123,
  until="final",  # or "initial" / "refined"
)

   

If your application can accept a quadrilateral that does not strictly include all input points, use the tighter initial guess with early stop:

initial = QuadrilateralFitter(polygon=your_noisy_polygon).fit(until="initial")

API Reference

QuadrilateralFitter(polygon)

Initialize the QuadrilateralFitter instance.

• polygon: np.ndarray | tuple | list | object. Coordinates of the input geometry. Preferred: np.ndarray of shape (N, 2) or list/tuple of (x, y). Also accepts objects exposing .exterior.coords or .coords (e.g., Shapely geometries) via duck‑typing. Shapely is NOT required at runtime.

QuadrilateralFitter.fit → tuple of 4 (x, y)

Signature:

QuadrilateralFitter.fit(
    simplify_polygons_larger_than: int | None = 10,
    start_simplification_epsilon: float = 0.1,
    max_simplification_epsilon: float = 0.5,
    simplification_epsilon_increment: float = 0.02,
    max_initial_combinations: int = 300,
    random_seed: int | None = None,
    until: Literal["initial", "refined", "final"] = "final",
    auto_scale_simplification: bool = True,
    max_points_for_refinement: int | None = None,
) -> tuple[tuple[float, float], tuple[float, float], tuple[float, float], tuple[float, float]]

• simplify_polygons_larger_than: If specified, performs a preliminary Douglas–Peucker simplification of the convex hull when it has more than this many vertices. This speeds up the process but may lead to a slightly sub‑optimal quadrilateral. Default: 10.
• start_simplification_epsilon, max_simplification_epsilon, simplification_epsilon_increment: Epsilon schedule for the Douglas–Peucker simplification.
• max_initial_combinations: Limits the number of candidate quadrilaterals tested when searching the initial guess. If 0 or larger than the total number of combinations C(N,4), a full search is performed. Otherwise, up to this many unique combinations are sampled randomly. Default: 300.
• random_seed: RNG seed for deterministic sampling when max_initial_combinations is used. Default: None.
• until: Choose how far the pipeline should run for performance. "initial" returns only the initial guess, skipping finetune/expansion. "refined" runs TLS finetuning but skips final expansion. "final" runs the full pipeline. Default: "final".
• auto_scale_simplification: If True, scales Douglas–Peucker epsilon parameters by the input size (bounding box diagonal) when epsilons look relative (<= 1). Helps keep simplification consistent across scales. Default: True.
• max_points_for_refinement: Optional cap for the number of points used in the TLS finetuning stage. If the input has more points, a deterministic subsample is used (or RNG with random_seed). This can dramatically reduce runtime on very large point clouds with minimal accuracy loss. Default: None (use all points).

Returns: A 4-vertex quadrilateral (counter-clockwise) for the requested stage:

• until="initial": best IoU vs convex hull (may not contain all points)
• until="refined": after TLS finetuning
• until="final": expanded to strictly contain the convex hull (default)

Real Case Example

Let's simulate a real case scenario where we detect a noisy polygon from a form that we know should be a perfect rectangle (only deformed by perspective).

import numpy as np
import cv2

image = cv2.cvtColor(cv2.imread('./resources/input_sample.jpg'), cv2.COLOR_BGR2RGB)   

# Save the Ground Truth corners
true_corners = np.array([[50., 100.], [370., 0.], [421., 550.], [0., 614.], [50., 100.]], dtype=np.float32)

# Generate a simulated noisy detection
sides = [np.linspace([x1, y1], [x2, y2], 20) + np.random.normal(scale=10, size=(20, 2))
         for (x1, y1), (x2, y2) in zip(true_corners[:-1], true_corners[1:])]
noisy_corners = np.concatenate(sides, axis=0)

# To simplify, we will clip the corners to be within the image
noisy_corners[:, 0] = np.clip(noisy_corners[:, 0], a_min=0., a_max=image.shape[1])
noisy_corners[:, 1] = np.clip(noisy_corners[:, 1], a_min=0., a_max=image.shape[0])

And now, let's run QuadrilateralFitter to find the quadrilateral that best approximates our noisy detection (without leaving points outside).

from quadfit import QuadrilateralFitter

# Define the fitter and compute desired stages
fitter = QuadrilateralFitter(polygon=noisy_corners)
fitted_quadrilateral = np.array(fitter.fit(until="final"), dtype=np.float32)
# Tighter quadrilateral (may exclude some points):
tight_quadrilateral = np.array(fitter.fit(until="initial"), dtype=np.float32)

     

Finally, for use cases like this, we could use fitted quadrilaterals to apply a perspective correction to the image, so we can get a visual insight of the results.

# Generate the destination points for the perspective correction by adjusting it to a perfect rectangle
h, w = image.shape[:2]

for quadrilateral in (fitted_quadrilateral, tight_quadrilateral):
    # Cast it to a numpy for agile manipulation
    quadrilateral = np.array(quadrilateral, dtype=np.float32)

    # Get the bounding box of the fitted quadrilateral
    min_x, min_y = np.min(quadrilateral, axis=0)
    max_x, max_y = np.max(quadrilateral, axis=0)

  # Define the destination points for the perspective correction
  destination_points = np.array(((min_x, min_y), (max_x, min_y),
                   (max_x, max_y), (min_x, max_y)), dtype=np.float32)

    # Calculate the homography matrix from the quadrilateral to the rectangle
  homography_matrix, _ = cv2.findHomography(srcPoints=quadrilateral, dstPoints=destination_points)
    # Warp the image using the homography matrix
    warped_image = cv2.warpPerspective(src=image, M=homography_matrix, dsize=(w, h))