-
Notifications
You must be signed in to change notification settings - Fork 0
Encoder Sensor
The encoder sensor works as any other sensor. You create the object that defines it (with the pins where it is connected, and the pointers to the variables you want to save the values on), then you use the start method (after all HALAL starts) which will define the point on time where the encoder starts counting. Then you just use the read method to get the values on the variables given on its constructor.
You need to do the read faster than the size of the frames, even if you don t need to update the values; otherwise the values won t be as precise.
The encoder sensor is coded in such a way that you can configurate it with your own preferences. You can trade speed, reaction time, and precision with the values of N_FRAMES and FRAME_SIZE_IN_SECONDS. You also need to configurate the encoder with the distance that represents a +1 in the counter of the encoder in COUNTER_DISTANCE_IN_METERS. This value depends on the encoder you are using, and also affects precision.
Each variable represents one thing:
- N_FRAMES: The number of frames the encoder saves on its array. The bigger it is, the bigger the size of the array, the better the precision the worse the reaction time and the more space the object takes
- FRAME_SIZE_IN_SECONDS: The period of each frame, the minimun time between its start and its end, in seconds. The bigger it is, the faster the read and the worse the precision and reaction time.
- COUNTER_DISTANCE_IN_METERS: As said abode, the number in real world that the encoder counter represents, in meters. The smaller the better, as it gives more precision (altough it reduces the range of representation)
And here is each formula for each thing these affect on:
The minimun difference on Position and the range of those it can represent. Both depend solely on the encoder
Position precision = COUNTER_DISTANCE_IN_METERS m
Position range = COUNTER_DISTANCE_IN_METERS * 32767 m
The minimun difference of Speed it can represent. If this value was 1 for example, it would only be able to represent integers (nothing between 0 and 1, or between 1 and 2...).
Speed precision = COUNTER_DISTANCE_IN_METERS * N_FRAMES * FRAME_SIZE_IN_SECONDS m/s
The time it takes to fully realise a change on speed or acceleration. If the Pod was going at 100 m/s and abruptly stopped, it will get the speed reduced each frame, and it will need its full reaction time to reach 0 m/s
Reaction time = N_FRAMES * FRAME_SIZE_IN_SECONDS s
Spatial cost = O(N_FRAMES)
Temporal cost = O(1 + N_FRAMES / FRAME_SIZE_IN_SECONDS)
Now its time to actually explain how the Encoder calculations work. First of all, we will define each value we want to return and how it should be calculated mathematically. Then we will explain the approximations and why did we take those.
First, the position and time are base quantities intrinsical to the objects. They cannot be calculated, as they are not derived values; they can only be detected. the speed and acceleration are derived quantities, which means that they cannot be detected on themselves, you can only detect their effects or sources and derive them with those.
Some sensors are able to obtain such values on themselves, but these just get some base quantities and then make the calculations. Accelerometers, for example, calculate acceleration by measuring the G force generated by the acceleration, which its itself measured by a piezoelectric that generates electrical tension when it suffers any force. So we supposedly want to obtain position and time directly and then derive speed and acceleration.
And we will literally derive the speed from the position and time, as the definition of speed is s = d p / d t, the time derivative of the position. The acceleration is the time derivative of the speed. We just have one problem. Derivative are operations defined on continuous functions, and computers aren t known by working on the continuous space. We could define such a space with some functions, and while we would get higher precision we would suffer on the efficiency side, as these definitions + the derivative could consume too much time, and we would end approximating it anyway.
We would use the backwards finite difference approximation. Finite difference means that its samples two points and measures their differences to approximate the tangent to the function. Backwards means that it only uses the actual value and the values behind it to make the calculation. It is a worse estimation than the central finite difference, but sadly the Encoder cannot give us his position in the future, as it lacks divination powers.
So we take the position we have now and the position we had some time before, substract those two, divide by the time difference and we have it. Thats our speed. As we can see, we need to save not only our actual position and time, but some position and time on the past. We also have to watch out that the distance on time isn t too low, as any spike on the measure (which we would always have as the encoder counts on whole numbers so it goes on steps) will be amplified; nor it can be too high as it would measure an average over a long time which wouldn t be a good estimate of the derivative. For that purpose we will save more than just one point on the past, so we can assure that the difference on time is less than the distance between these points saved. We called this time FRAME_SIZE_IN_SECONDS, and the amount of points saved N_FRAMES. The distance on time from past point to actual point would be in the range of (FRAME_SIZE_IN_SECONDS * N_FRAMES, FRAME_SIZE_IN_SECONDS * (N_FRAMES + 1)).
The acceleration uses the same operations but changing position by the values calculated on the speed formula. This means that the calculation on acceleration has more overhead and worse reaction time, as it suffers its own plus the one on the speed values it takes.
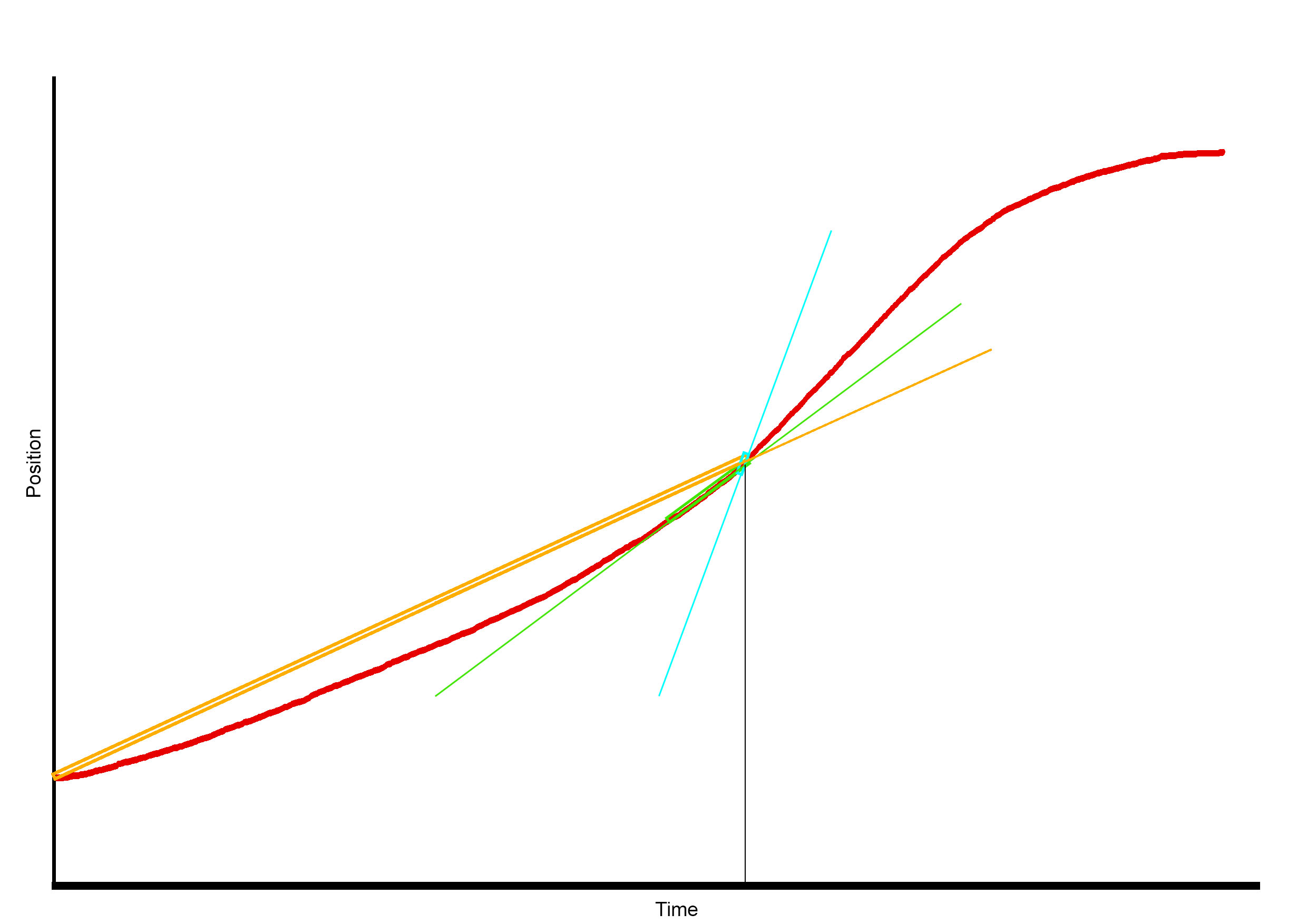
Here we have an example of the calculation given a point in time. The rectangles mark the two points used for the calculations and the lines are the result of those. Orange is when the time between the past point and the actual point is too much. Blue on the other side represents what happens when it is too little (the rectangle doesn t correctly adjust to the graphic as the encoder cannot exactly represent the value, so this happens). The green is the point where we smooth these slopes and spikes enough without losing information.
https://en.wikipedia.org/wiki/Physical_quantity
