Tsallis Divergence Is Not Bounded Below Consistently. #27
Description
Problem: Tsallis Divergence is not lower-bounded, hence minimization will leads towards negative infinity.
Definition The Tsallis Divergence is defined as :
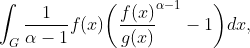
where if alpha approaches one then this approaches the Kullback-Leibler. This can be proven by using L Hopital rule (since bottom and top evaluate to zero then we satisfy L Hopital assumption) and showing that
Plotting this, it does seem to approach it.
Implementation: I'm putting in the constraint that the integral should match. I'm use mask value of 1e-12 to g(x) from the division of f(x) with g(x) and set the ratio (f(x)/g(x)) to zero if g(x) < 1e-12.
Choosing Alpha
- Choosing alpha to be very tight, 1.0000001, after 13 iterations with trust-constraint, it got to -4.0983e+04 Tsallis and KL value of infinity (model density is negative somwhere).
- Choosing alpha to be 1.0001, then I see a lower-bound. I also see this when I plot it. After 84 iterations with trust-constraint, Tsallis value converged to +2.7715e-02 with KL value of 0.0415.
- Choosing alpha < 1, we get that it is approaching logarithm from below and hence will not be lower-bounded, turst-constr gives -infinity as objective value.
- Choosing 1.00001 after 157 iterations, trust constraint region method seems to convergence to Tsallis value of -0.145, and KL value of 0.069285
Reference
[1] - Paul "Information Theory, the shape function and the Hirshfield atom"
[2] - Farnaz "Hirshfield partioning from non-extensive entropies"
Going to do: I'm going to run these alpha for longer periods of time.